Home /
Expert Answers /
Statistics and Probability /
y-a-e-b-t-3-points-let-39-s-say-you-collected-some-noisy-data-see-below-that-you-hypothesized-pa478
(Solved): y=a*e^((-b*t)) (3 points) Let's say you collected some noisy data (see below) that you hypothesized ...
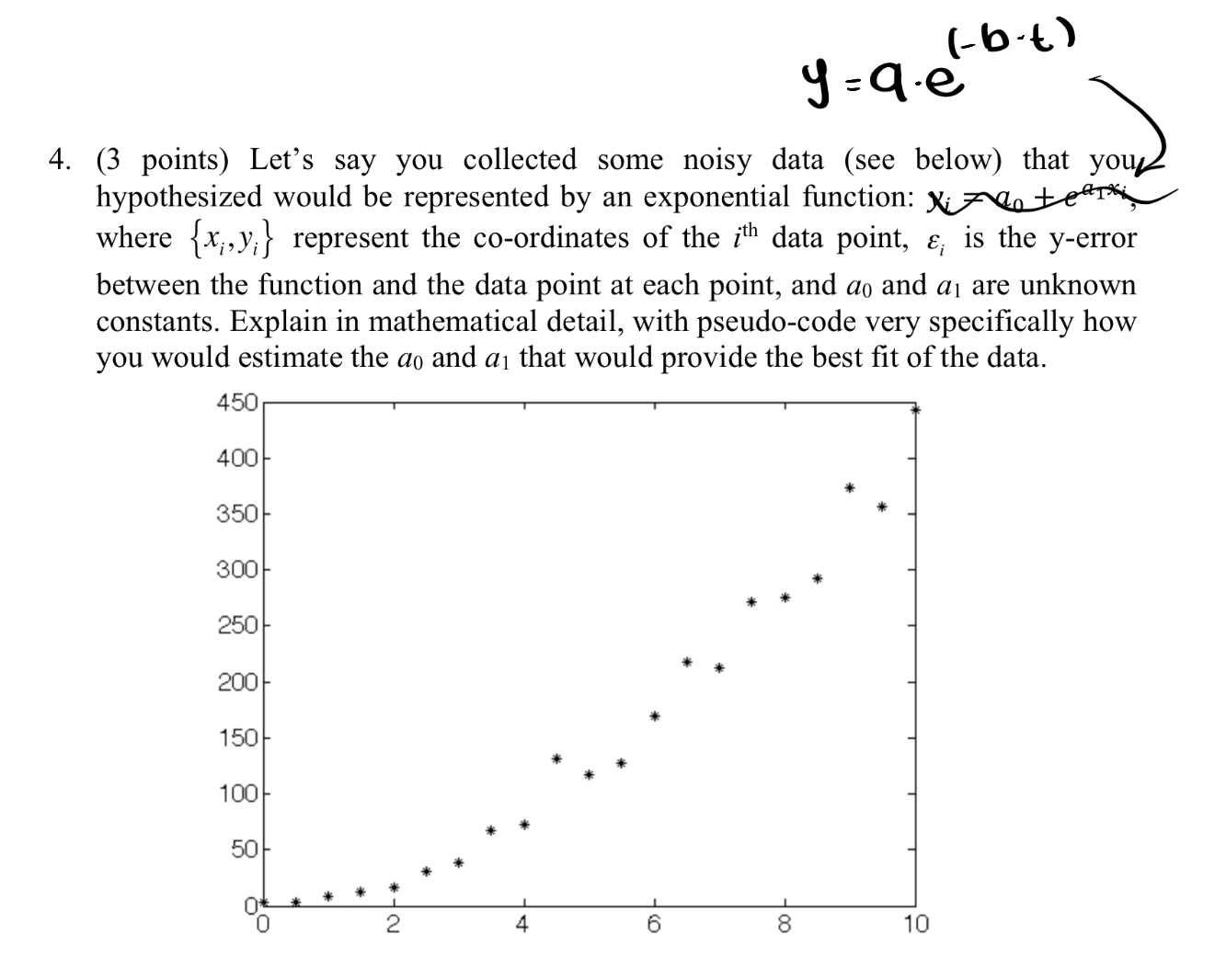
y=a*e^((-b*t))
(3 points) Let's say you collected some noisy data (see below) that you
hypothesized would be represented by an exponential function:
where {x_(i),y_(i)} represent the co-ordinates of the i^(th ) data point, \epsi _(i) is the y-error
between the function and the data point at each point, and a_(0) and a_(1) are unknown
constants. Explain in mathematical detail, with pseudo-code very specifically how
you would estimate the a_(0) and a_(1) that would provide the best fit of the data.