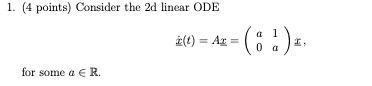(Solved): 1. (4 points) Consider the 2d linear ODE x(t)=Ax=(a01a)x, for some a ...

1. (4 points) Consider the $$2\mathrm{d}$$ linear $$\mathrm{ODE}$$ $$\underline{\underline{x}}(t)=A\underline{\underline{x}}=\left(\begin{array}{ll}a& 1\\ 0& a\end{array}\right)\underline{\underline{x}},$$ for some $$a?\mathbb{R}$$. (c) Suppose $$a<0$$. Plot the vector field and some representative solutions of this system. Is $$x^{?}=(0,0)$$ an attractive point or just neutrally stable? Also, plot the vector field and solutions of $$\underline{\underline{x}}=\left(\begin{array}{ll}a& 0\\ 0& a\end{array}\right)\underline{\underline{x}}$$. What is the main difference between these two plots? In the dynamical systems lingo, the former is called a degenerate node and the latter a star node. (d) In class, we discussed various linear systems as characterized by their trace and determinant ( $$?$$ and $$?$$, respectively). Which set in the $$???$$ plane represents star nodes and degenerate nodes? Can we distinguish between star and degenrate nodes given $$?$$ and $$?$$ alone? Why?