(Solved): 1. A survey of 25 randomly selected customers found the ages shown (in years). The mean is 32.16 y ...

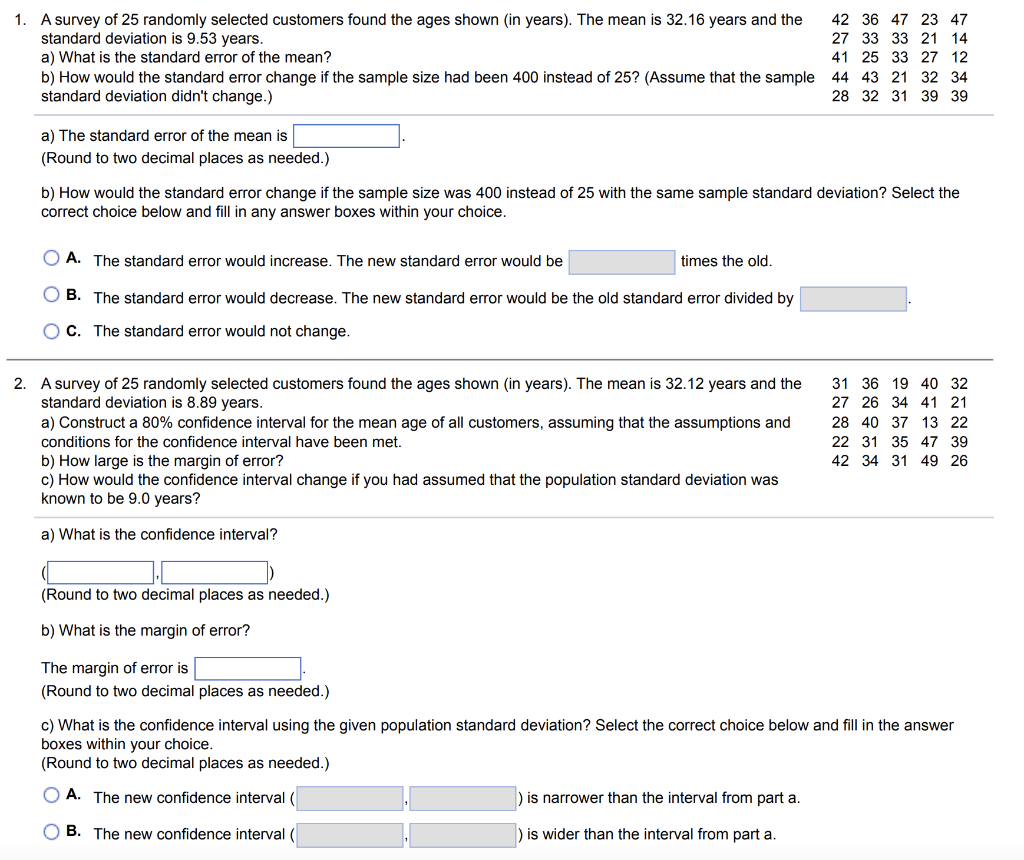
1. A survey of 25 randomly selected customers found the ages shown (in years). The mean is 32.16 years and the standard deviation is 9.53 years. a) What is the standard error of the mean? b) How would the standard error change if the sample size had been 400 instead of 25 ? (Assume that the sample standard deviation didn't change.) a) The standard error of the mean is (Round to two decimal places as needed.) b) How would the standard error change if the sample size was 400 instead of 25 with the same sample standard deviation? Select the correct choice below and fill in any answer boxes within your choice. A. The standard error would increase. The new standard error would be times the old. B. The standard error would decrease. The new standard error would be the old standard error divided by C. The standard error would not change. 2. A survey of 25 randomly selected customers found the ages shown (in years). The mean is 32.12 years and the $$3136194032$$ standard deviation is 8.89 years. a) Construct a $$80\%$$ confidence interval for the mean age of all customers, assuming that the assumptions and $$28403722$$ conditions for the confidence interval have been met. b) How large is the margin of error? c) How would the confidence interval change if you had assumed that the population standard deviation was known to be 9.0 years? a) What is the confidence interval? $$11$$ (Round to two decimal places as needed.) b) What is the margin of error? The margin of error is (Round to two decimal places as needed.) c) What is the confidence interval using the given population standard deviation? Select the correct choice below and fill in the answer boxes within your choice. (Round to two decimal places as needed.) A. The new confidence interval ( ) is narrower than the interval from part a. B. The new confidence interval ( ) is wider than the interval from part a.