(Solved): 1. By convention, what are the positive directions for normal stress and shear stress? For this qu ...

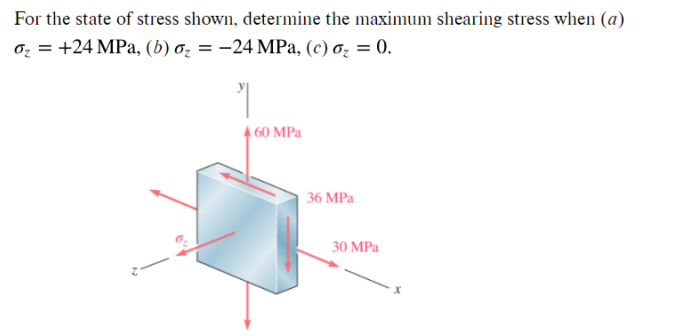
1. By convention, what are the positive directions for normal stress and shear stress? For this question, what do the values, \( 60 \mathrm{MPa}, 36 \mathrm{MPa} \) and \( 30 \mathrm{MPa} \), represent? Are they positive or negative according to the sign conventions? 2. For each value of \( \sigma_{z} \) in the problem statement, would we need to consider stress transformation in 2-D or 3-D? How many Mohr's circle(s) would you need to draw in each case? If there are multiple Mohr's circles, what do they each represent and how do they relate to each other? 3. How many maximum shear stresses exist for this stress element? What is the meaning or physical significance of each maximum shear stress? What equations can you use to calculate each maximum shear stress? What does each parameter in the equations represent? 4. Is the \( \sigma_{z} \) a principal stress? Will the specific values of the \( \sigma_{z} \) change whether or not it is a principal stress or not? Why or why not? 5. To determine the principal stresses within the \( x-y \) plane, are you able to consider only one projected view of the 3-D stress element? If so, how would you construct the relevant Mohr's circle? 6. Try to construct the Mohr's circle(s) for case (a) as a single diagram. Clearly label each circle - the corresponding plane of the stress element, radius, principle stresses, maximum in-plane shear stress, and absolute maximum shear stress if applicable. For the state of stress shown, determine the maximum shearing stress when \( (a) \) \[ \sigma_{z}=+24 \mathrm{MPa},(b) \sigma_{z}=-24 \mathrm{MPa},(c) \sigma_{z}=0 \]