(Solved): 1. Connect all sections of the load modules in parallel. Set up the circuit s ...

???????

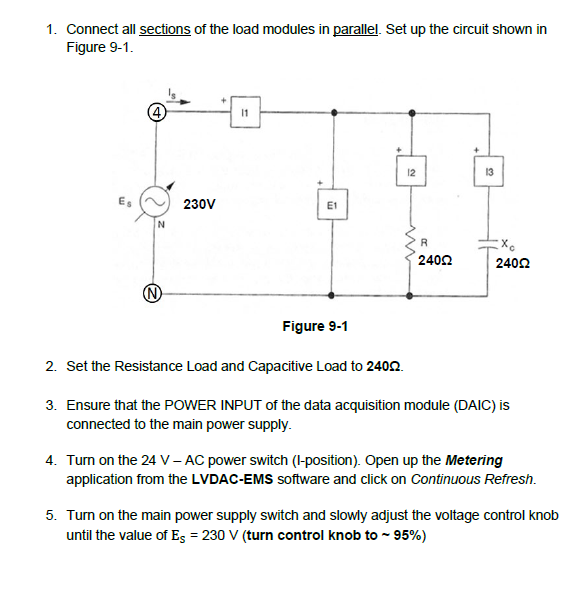
1. Connect all sections of the load modules in parallel. Set up the circuit shown in Figure 9-1. Figure 9-1 2. Set the Resistance Load and Capacitive Load to \( 240 \Omega \). 3. Ensure that the POWER INPUT of the data acquisition module (DAIC) is connected to the main power supply. 4. Turn on the \( 24 \mathrm{~V}-\mathrm{AC} \) power switch (I-position). Open up the Metering application from the LVDAC-EMS software and click on Continuous Refresh. 5. Turn on the main power supply switch and slowly adjust the voltage control knob until the value of \( E_{S}=230 \mathrm{~V} \) (turn control knob to 95\%) 6. Measure the circuit currents and note the results below. \[ \begin{array}{ll} \mathrm{I}_{\mathrm{S}}=\mathrm{I}_{1}= \\ \mathrm{I}_{\mathrm{R}}=\mathrm{I}_{2}= \\ \mathrm{I}_{\mathrm{C}}=\mathrm{I}_{3}= & \mathrm{A} \\ \mathrm{A} \end{array} \] 7. Determine the sum of \( \mathrm{I}_{\mathrm{R}} \) and \( \mathrm{I}_{\mathrm{C}} \). \[ \mathrm{I}_{\mathrm{R}}+\mathrm{I}_{\mathrm{C}}=\square \mathrm{A} \] 8. Does the sum of the branch currents equal the measured value of the source current, \( \mathrm{I}_{\mathrm{S}} \) ? Why? 9. Calculate the magnitude of the vector sum representing the source current, and the phase angle of the source. \[ \mathrm{I}_{\mathrm{S}}=\sqrt{\mathrm{I}_{\mathrm{R}}{ }^{2}+\mathrm{I}_{\mathrm{C}}{ }^{2}}=\quad \mathrm{A} \quad \phi=\tan ^{-1} \frac{\mathrm{I}_{\mathrm{C}}}{\mathrm{I}_{\mathrm{R}}}= \] 10. Click on the Phasor Analyzer and display the three phasors; \( \mathrm{I}_{\mathrm{S}}, \mathrm{I}_{\mathrm{R}} \), and \( \mathrm{I}_{\mathrm{L}} \) on channels I1, 12 and 13 respectively (Set current scale to \( 0.5 \mathrm{~A} / \mathrm{div} \) ). Include the reference phasor, \( \mathrm{E}_{\mathrm{S}} \) on channel \( \mathrm{E} \) 1. Does the phasor diagram show that \( \mathrm{I}_{\mathrm{S}} \) is the vector sum of \( \mathrm{I}_{\mathrm{R}} \) and \( \mathrm{I}_{\mathrm{C}} \) ? \[ \text { Yes } \quad \square \text { No } \] 11.Are the results of your calculations in step 10 approximately equal to the values of magnitude and phase of Is shown in the Phasor Analyzer? \( \square \) Yes \( \quad \square \) No