(Solved): 15.4 Let \( f(x, y)=e^{-x y} \sin x \sin y \) if \( x \geq 0, y \geq 0 \), and let \( f(x, y)=0 \) ...

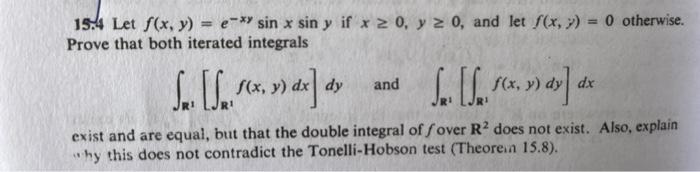
15.4 Let \( f(x, y)=e^{-x y} \sin x \sin y \) if \( x \geq 0, y \geq 0 \), and let \( f(x, y)=0 \) otherwise. Prove that both iterated integrals \[ \int_{\mathbf{R}^{1}}\left[\int_{\mathbf{R}^{1}} f(x, y) d x\right] d y \quad \int_{\mathbf{R}^{1}}\left[\int_{\mathbf{R}^{1}} f(x, y) d y\right] d x \] exist and are equal, but that the double integral of \( f \) over \( \mathbf{R}^{2} \) does not exist. Also, explain why this does not contradict the Tonelli-Hobson test (Theorein \( 15.8 \) ).