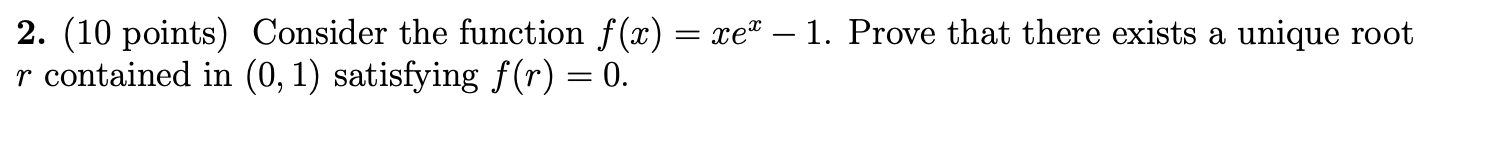Home / Expert Answers / Computer Science / 2-10-points-consider-the-function-f-x-xex1-prove-that-there-exists-a-unique-root-r-contain-pa957

(Solved): 2. (10 points) Consider the function f(x)=xex1. Prove that there exists a unique root r contain ...


2. (10 points) Consider the function \( f(x)=x e^{x}-1 \). Prove that there exists a unique root \( r \) contained in \( (0,1

2. (10 points) Consider the function . Prove that there exists a unique root contained in satisfying .


We have an Answer from Expert

View Expert Answer

Expert Answer

Ans:-To show the existence and uniqueness of a root T of the functionf(x)=x?eA×?1 in th
We have an Answer from Expert

Buy This Answer $5

Place Order

We Provide Services Across The Globe

Order Now
Go To Answered Questions