(Solved): (2) Graph Connectivity Recall that the eigenvalues of the Laplacian of a graph on n vertices can b ...

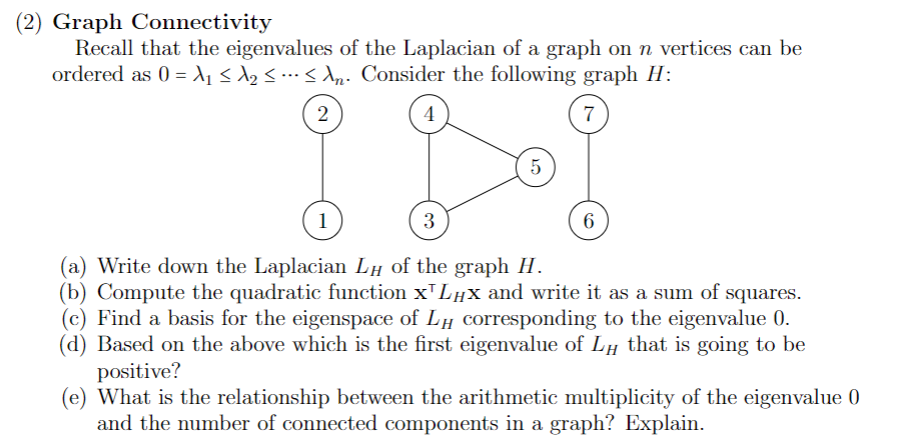
(2) Graph Connectivity Recall that the eigenvalues of the Laplacian of a graph on

vertices can be ordered as

. Consider the following graph

: (a) Write down the Laplacian

of the graph

. (b) Compute the quadratic function

and write it as a sum of squares. (c) Find a basis for the eigenspace of

corresponding to the eigenvalue 0 . (d) Based on the above which is the first eigenvalue of

that is going to be positive? (e) What is the relationship between the arithmetic multiplicity of the eigenvalue 0 and the number of connected components in a graph? Explain.