2. In this problem we outline a proof of Theorem 7.4.3 in the case n=2. Let x(1) and x(2) be solutions of Eq. (3) for

Question

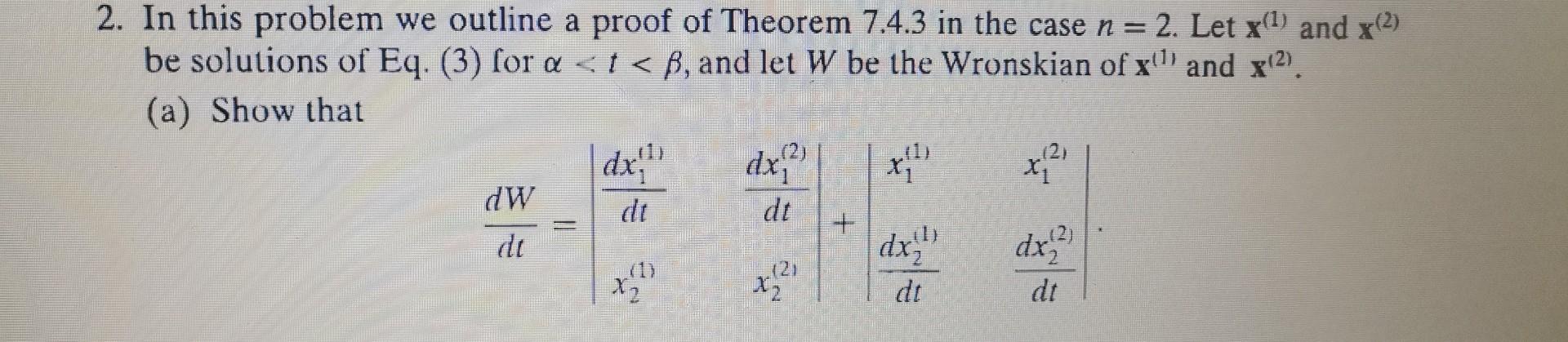
2. In this problem we outline a proof of Theorem 7.4.3 in the case n=2. Let x(1) and x(2) be solutions of Eq. (3) for <t<, and let W be the Wronskian of x(1) and x(2). (a) Show that dtdW=dtdx1(1)x2(1)dtdx1(2)x2(2)+x1(1)dtdx2(1)x1(2)dtdx2(2).  (b) Using Eq. (3), show that dtdW=(p11+p22)W (c) Find W(t) by solving the differential equation obtained in part (b). Use this expression to obtain the conclusion stated in Theorem 7.4.3.

Accepted Answer

Expert Answer to -          2. In this problem we outline a proof of Theorem 7.4.3 in the case n=2. Let x(1) and x(2) b

Answer

Solution for -          2. In this problem we outline a proof of Theorem 7.4.3 in the case n=2. Let x(1) and x(2) b

Answer

This an additional answer to -          2. In this problem we outline a proof of Theorem 7.4.3 in the case n=2. Let x(1) and x(2) b

(Solved): 2. In this problem we outline a proof of Theorem 7.4.3 in the case n=2. Let x(1) and x(2) b ...

View Expert Answer

Expert Answer

Buy This Answer $5

Place Order

We Provide Services Across The Globe