(Solved): 2 part question  EXAMPLE 4 Graph the function \( f(x)=\sin 50 x \) in an apprepriate viewing ro ...

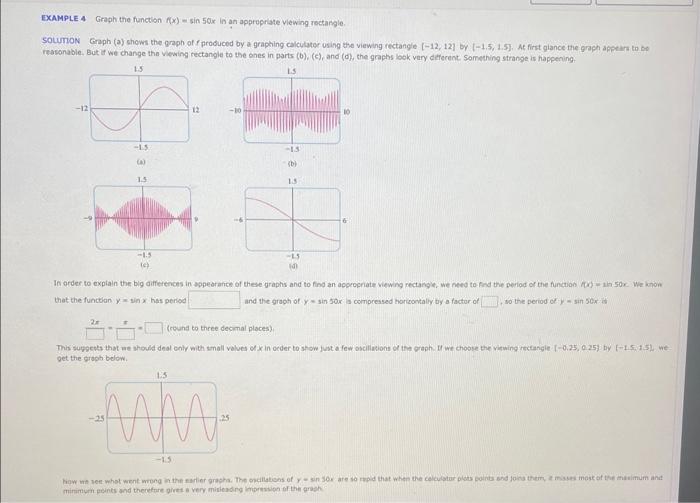
EXAMPLE 4 Graph the function \( f(x)=\sin 50 x \) in an apprepriate viewing roctangle. SOUUTION Graph \( (a) \) shows the gaph of \( f \) produced by a graphing calculator using the viewing rectangle. \( [-12,12] \) by \( [-1,5,1.5] \). At first giance the graph appe irs to bo ressonable, But if we change the vewing tectangle to the ones in parts (b), (c), and (d), the graphs look vary deterent, Something strange is happening that the functian \( y=\sin x \) his period and the graph of \( y=\sin 30 x \) a compressed horicontaliy ty a factor of to the period of \( y=\sin 50 x \) is get the graph below. The equation \( \cos x=x \) has exactly one solution. (a) Use a graph to show that the equation \( \cos x \) in \( 0.3 x \) has three solutions and find their values correct to two decirnal places. \[ \begin{array}{ll} x= & \text { (smallest value) } \\ x= \\ x= & \text { (largest yalue) } \end{array} \] (b) Find an approximate yalue of \( m \) soch that the equation cos \( x \). \( m x \) has oxactly two solutions. (Round your answers to four decimal places.) \[ \begin{array}{ll} m= & \text { (smaller value) } \\ m= & \text { (Lamger value) } \end{array} \]