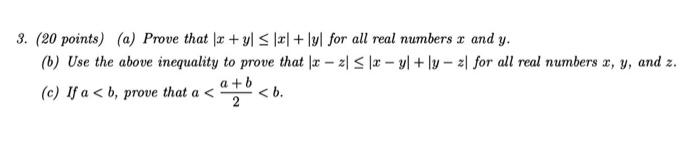Home /
Expert Answers /
Advanced Math /
3-20-points-a-prove-that-x-yx-y-for-all-real-numbers-x-and-y-b-use-the-pa331
Expert Answer
In order to solve part a. we will have to first let |x+y| = a, and the and now we will check the conditions for 4 cases:case 1: let x=1 and y=2|a|=<=|x|+|y|put in the values; Hence for all values of x,y which are greater than or equal to 0 will satisfy the given equation.Now Case 2: now let x ne -2 and y be -1so now putting it all in the equation will be: And now we will have to check case 3:Where x<=0 and y>=0 so we will let x be -1 and y be 1.by putting the values in the equation we will get:- hence this case is also correctFinally we will check for case 4:where x>=0 and y<=0So now we will assume x=1 and y=-1now by putting the values in the equation we will get: hence after checking all 4 cases we can conclude that for any real values of x and y the condition given to us is true.