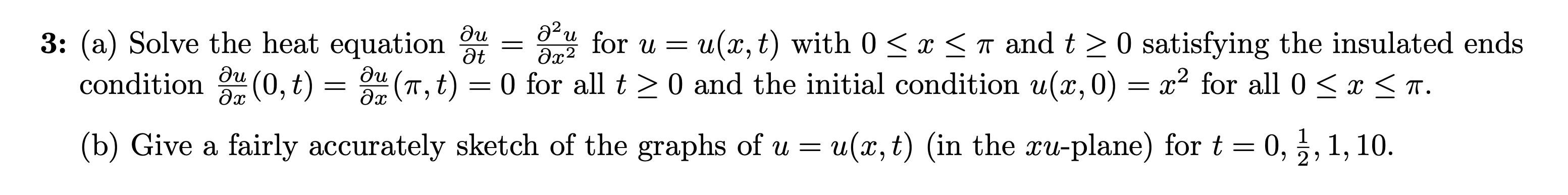Home /
Expert Answers /
Advanced Math /
3-a-solve-the-heat-equation-delu-delt-del-2-u-delx-2-for-u-u-x-t-with-0-lt-x-lt-p-pa803
(Solved): 3: (a) Solve the heat equation (delu)/(delt)=(del^(2)u)/(delx^(2)) for u=u(x,t) with 0<=x<=\p ...
3: (a) Solve the heat equation
(delu)/(delt)=(del^(2)u)/(delx^(2))for
u=u(x,t)with
0<=x<=\pi and
t>=0satisfying the insulated ends condition
(delu)/(delx)(0,t)=(delu)/(delx)(\pi ,t)=0for all
t>=0and the initial condition
u(x,0)=x^(2)for all
0<=x<=\pi . (b) Give a fairly accurately sketch of the graphs of
u=u(x,t)(in the
xu-plane) for
t=0,(1)/(2),1,10.