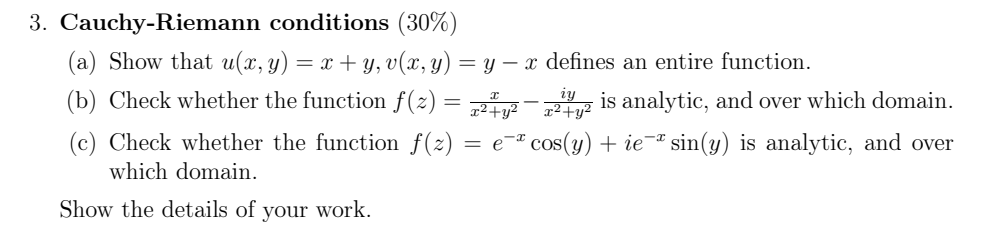(Solved): 3. Cauchy-Riemann conditions (30\%) (a) Show that \( u(x, y)=x+y, v(x, y)=y-x \) defines an entire ...

3. Cauchy-Riemann conditions (30\%) (a) Show that \( u(x, y)=x+y, v(x, y)=y-x \) defines an entire function. (b) Check whether the function \( f(z)=\frac{x}{x^{2}+y^{2}}-\frac{i y}{x^{2}+y^{2}} \) is analytic, and over which domain. (c) Check whether the function \( f(z)=e^{-x} \cos (y)+i e^{-x} \sin (y) \) is analytic, and over which domain. Show the details of your work.