(Solved): 3. Let \( U=\left\{\mathbf{u}_{1}, \mathbf{u}_{2}\right\} \) and \( \mathcal{W}=\left\{\mathbf{w}_{ ...

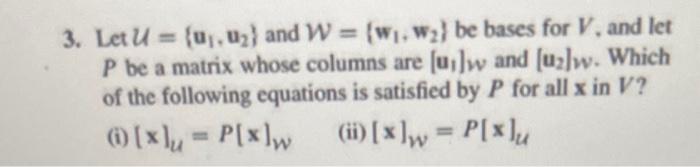
3. Let \( U=\left\{\mathbf{u}_{1}, \mathbf{u}_{2}\right\} \) and \( \mathcal{W}=\left\{\mathbf{w}_{1}, \mathbf{w}_{2}\right\} \) be bases for \( V \), and let \( P \) be a matrix whose columns are \( \left[\mathbf{u}_{1}\right] w \) and \( \left[\mathbf{u}_{2}\right] w \). Which of the following equations is satisfied by \( P \) for all \( \mathrm{x} \) in \( V \) ? (i) \( [\mathrm{x}]_{U}=P[\mathbf{x}]_{W} \) (ii) \( [\mathbf{x}]_{w}=P[\mathbf{x}]_{U} \)