(Solved): 3rd time posting these questions an no one wants to help! i need it i be paying to learn and my assi ...

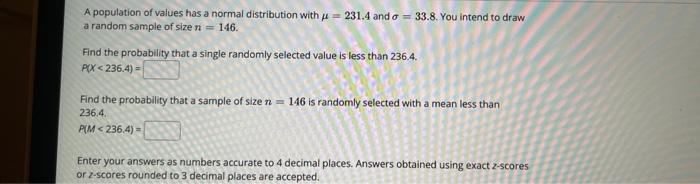
A.population of values has a normal distribution with \( \mu=231.4 \) and \( \sigma=33.8 \). You intend to draw a random sample of size \( n=146 \). Find the probablity that a single randomly selected value is less than \( 236.4 . \) \( P(x<236.4)= \) Find the probability that a sample of size \( n=146 \) is randomly selected with a mean less than \( 236.4 . \) \[ P(M<236.4)= \] Enter your answers as numbers accurate to 4 decimal places. Answers obtained using exact z-scores or 2 -scores rounded to 3 decimal places are accepted. A population of values has a normal distribution with \( \mu=17.8 \) and \( \sigma=30.9 \). You intend to draw a random sample of size \( n=205 \). Find the probability that a single randomly selected value is between \( 11.3 \) and \( 20.4 \). \( P(11.3547.9)= \] Enter your answer as a number accurate to 4 decimal places. NOTE: Answers obtained using exact z. scores or \( z-5 \) cores rounded to 3 decimal places are accepted. If 16 of the men are randomly selected, find the probability that their mean score is at least \( 547.9 . \) \( P(M>547.9)= \) Enter your answer as a number accurate to 4 decimal places. NOTE: Answers obtained using exact z. scores or z-scores rounded to 3 decimal places are accepted. If the random sample of 16 men does result in a mean score of \( 547.9 \), is there strong evidence to support the claim that the course is jictually effective? Yes. The probability indicates that is is (highly ?) unlikely that by chance, a randomly selected group of students would get a mean as high as \( 547.9 . \) No. The probability indicates that is is possible by chance alone to randomly select a group of students with a mean as high as \( 547.9 . \) A company produces steel rods. The lengths of the steel rods are normally distributed with a mean of 163.6-cm and a standard deviation of \( 0.7-\mathrm{cm} \). For shipment, 10 steel rods are bundled together. Find the probability that the average length of a randomly selected bundle of steel rods is between 163.2-cm and \( 163.5-\mathrm{cm} \). \[ P(163.2-\mathrm{cm}