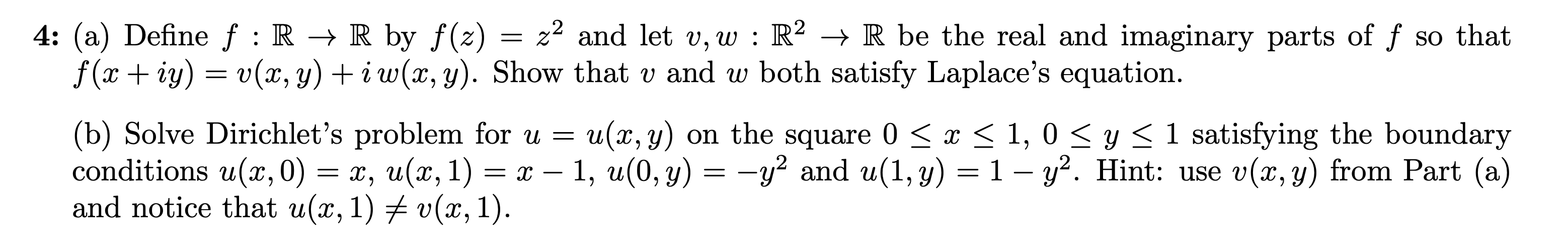Home /
Expert Answers /
Advanced Math /
4-a-define-f-r-gt-r-by-f-z-z-2-and-let-v-w-r-2-gt-r-be-the-real-and-imaginary-parts-of-f-pa860
(Solved): 4: (a) Define f:R->R by f(z)=z^(2) and let v,w:R^(2)->R be the real and imaginary parts of f ...
4: (a) Define
f:R->Rby
f(z)=z^(2)and let
v,w:R^(2)->Rbe the real and imaginary parts of
fso that
f(x+iy)=v(x,y)+iw(x,y). Show that
vand
wboth satisfy Laplace's equation. (b) Solve Dirichlet's problem for
u=u(x,y)on the square
0<=x<=1,0<=y<=1satisfying the boundary conditions
u(x,0)=x,u(x,1)=x-1,u(0,y)=-y^(2)and
u(1,y)=1-y^(2). Hint: use
v(x,y)from Part (a) and notice that
u(x,1)!=v(x,1).