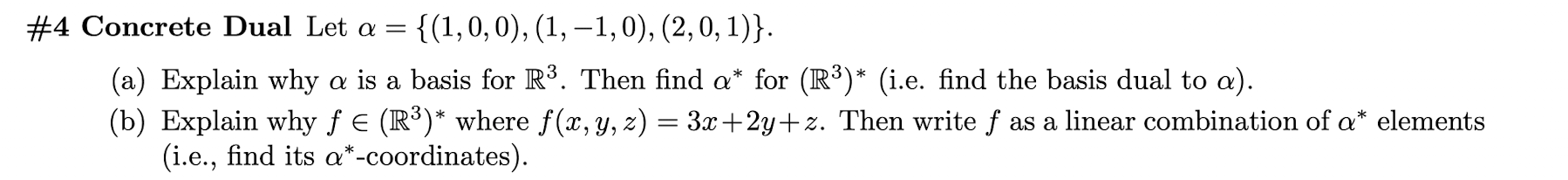(Solved): #4 Concrete Dual Let \( \alpha=\{(1,0,0),(1,-1,0),(2,0,1)\} \). (a) Explain why \( \alpha \) is a ...

#4 Concrete Dual Let \( \alpha=\{(1,0,0),(1,-1,0),(2,0,1)\} \). (a) Explain why \( \alpha \) is a basis for \( \mathbb{R}^{3} \). Then find \( \alpha^{*} \) for \( \left(\mathbb{R}^{3}\right)^{*} \) (i.e. find the basis dual to \( \alpha \) ). (b) Explain why \( f \in\left(\mathbb{R}^{3}\right)^{*} \) where \( f(x, y, z)=3 x+2 y+z \). Then write \( f \) as a linear combination of \( \alpha^{*} \) elements (i.e., find its \( \alpha^{*} \)-coordinates).