(Solved): A company sells sets of kitchen knives. A Basic Set consists of 2 utility knives and 1 chef's knife ...

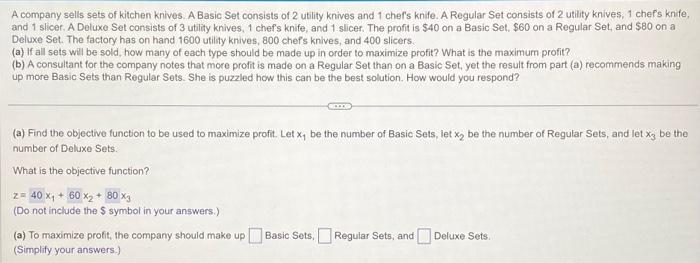
A company sells sets of kitchen knives. A Basic Set consists of 2 utility knives and 1 chef's knife. A Regular Set consists of 2 utility knives, 1 chef's knife, and 1 slicer. A Deluxe Set consists of 3 utility knives, 1 chefs knife, and 1 slicer. The profit is $\$40$ on a $B$ asic $\$$ Set, $\$60$ on a Regular Set, and $\$80$ on a Deluxe Set. The factory has on hand 1600 utility knives, 800 chef's knives, and 400 slicers. (a) If all sets will be sold, how many of each type should be made up in order to maximize profit? What is the maximum profit? (b) A consultant for the company notes that more profit is made on a Regular Set than on a Basic Set, yet the result from part (a) recommends making up more Basic. Sets than Regular Sets. She is puzzled how this can be the best solution. How would you respond? (a) Find the objective function to be used to maximize profit. Let $x_1$ be the number of Basic Sets, let $x_2$ be the number of Regular Sets, and let $x_3$ be the number of Deluxe Sets: What is the objective function? $z=40x_1+60x_2+80x_3$ (Do not include the $\$$ symbol in your answers.) (a) To maximize profit, the company should make up Basic Sets, Regular Sets, and Deluxe Sets. (Simplify your answers.)