Home /
Expert Answers /
Mechanical Engineering /
a-counter-flow-plate-exchanger-has-alternating-cold-hot-cold-hot-cold-narrow-rectangular-channel-pa763
(Solved): A counter-flow plate exchanger has alternating cold-hot-cold-...-hot-cold narrow rectangular channel ...
A counter-flow plate exchanger has alternating cold-hot-cold-...-hot-cold narrow rectangular
channels, built with plates of size L\times L separated by a distance a≪L. The hot flow is split
into N-1 channels and the cold flow is split into N channels. We will take L=15cm and
a=0.1cm, and will explore a few cases for N.
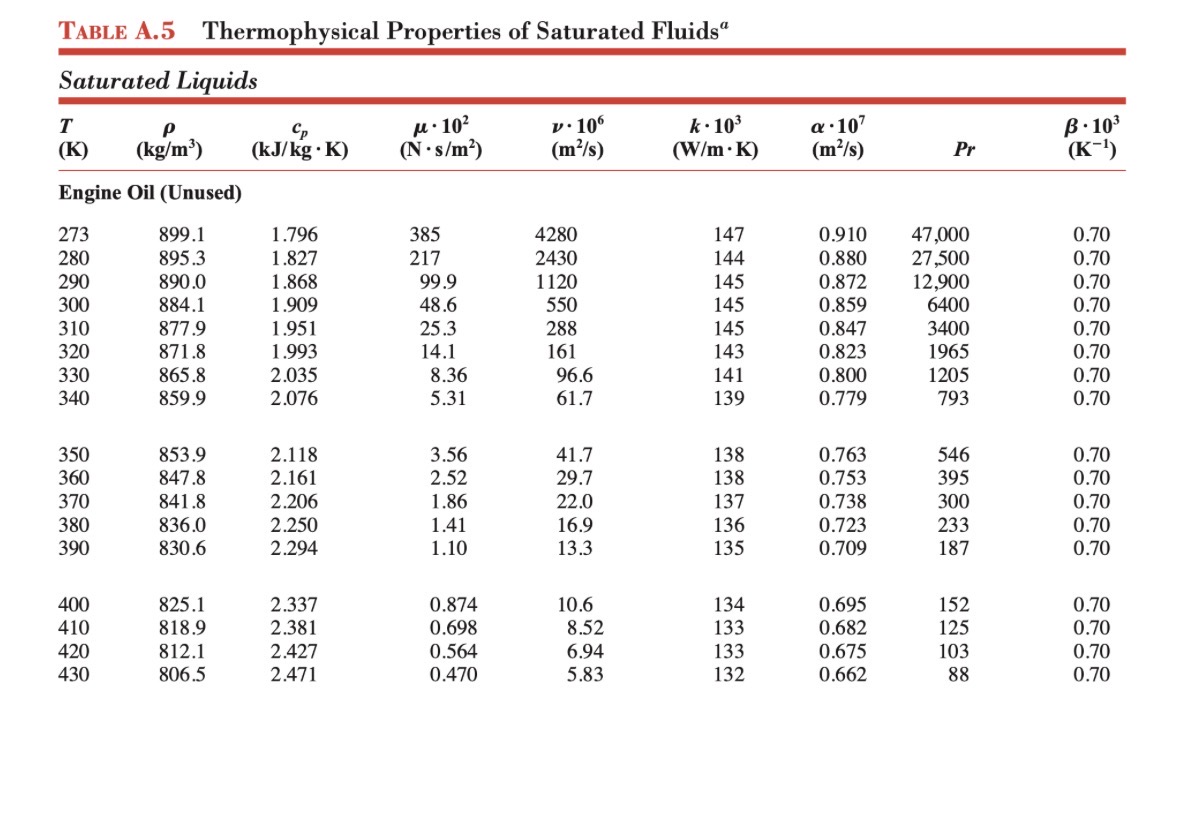
The hot flow is oil at 0.1k(g)/(s), with an inlet temperature of 100\deg C. We seek to reduce the
temperature of the oil to less than 50\deg C using a water source at 20\deg C, with the flow rate of
the water to be determined. Properties of oil are posted on Canvas.
Our design target can be achieved either with a large number of plates and lower cold flow
rate, or a lower number of plates and a higher cold flow rate - the design decision will depend
on cost an(d)/(o)r space constraints. Let's explore three options: N=8,12, and 16 . For each
case, determine m_(C)^(˙) and the power needed for pumping.
Three hints:
The total heat transfer area is A=(2N-2)L^(2) which comes from there being N+(N-1)
channels and therefore N+(N-1)-1=2N-2 heat transfer surfaces.
The power needed to pump the oil will be the same in all three cases.
You may assume laminar flow, and the oil flow will likely be the one in C_(min ).
Some possibly relevant equations... you might not use both. For a counterflow:
\epsi lon=(1-exp(-NTU(1-C_(r))))/(1-C_(r)exp(-NTU(1-C_(r)))),NTU=(1)/(C_(r)-1)ln((\epsi lon-1)/(\epsi lonC_(r)-1)) T