(Solved): (a) Find the approximations T_(10) and M_(10) for \int_1^2 31e^((1)/(x))dx. (Round your answers to s ...
(a) Find the approximations
T_(10)and
M_(10)for
\int_1^2 31e^((1)/(x))dx. (Round your answers to six decimal places.)
T_(10)=
M_(10)=
q,
◻(b) Estimate the errors in the approximations of part (a) using the smallest possible value for
Kaccording to the theorem about error bounds for trapezoidal and midpoint rules. (Round your answers to six decimal places.)
|E_(T)|<=
|E_(M)|<=
q,
◻(c) Using the values of
Kfrom part (b), how large do we have to choose
nso that the approximations
T_(n)and
M_(n)to the integral in part (a) are accurate to within 0.0001 ? For
T_(n^(')),n=
x. For
M_(n^('))n=
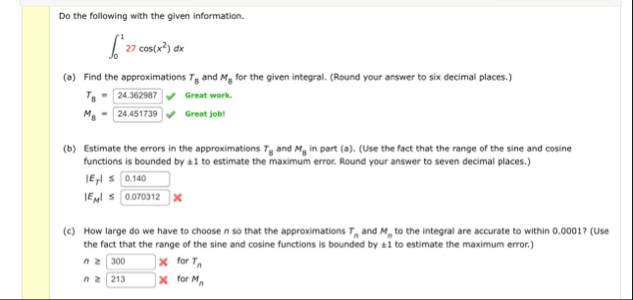
x. Do the following with the given information.
\int_0^1 27cos(x^(2))dx(a) Find the approximations
T_(8)and
M_(8)for the given integral. (Round your answer to six decimal places.)
T_(8)=,✓ Great work.
M_(8)=,✓ Great jobt (b) Estimate the errors in the approximations
T_(8)and
M_(8)in part (a). (Use the fact that the range of the sine and cosine functions is bounded by
!=1to estimate the maximum error. Round your answer to seven decimal places.)
|E_(T)|<=
|E_(M)|<=
q,
q,(c) How large do we have to choose
nso that the approximations
T_(n)and
M_(n)to the integral are accurate to within 0.0001 ? (Use the fact that the range of the sine and cosine functions is bounded by
-1to estimate the maximum error.)
n>=
q,
\times for
T_(n)
n>=
◻
\times for
M_(n)