Home /
Expert Answers /
Calculus /
a-firm-has-the-marginal-profit-function-dp-dx-12-000-6000x-x-2-4x-5-2-where-p-x-is-t-pa820
(Solved): A firm has the marginal-profit function (dP)/(dx)=(12,000-6000x)/((x^(2)-4x+5)^(2)), where P(x) is t ...
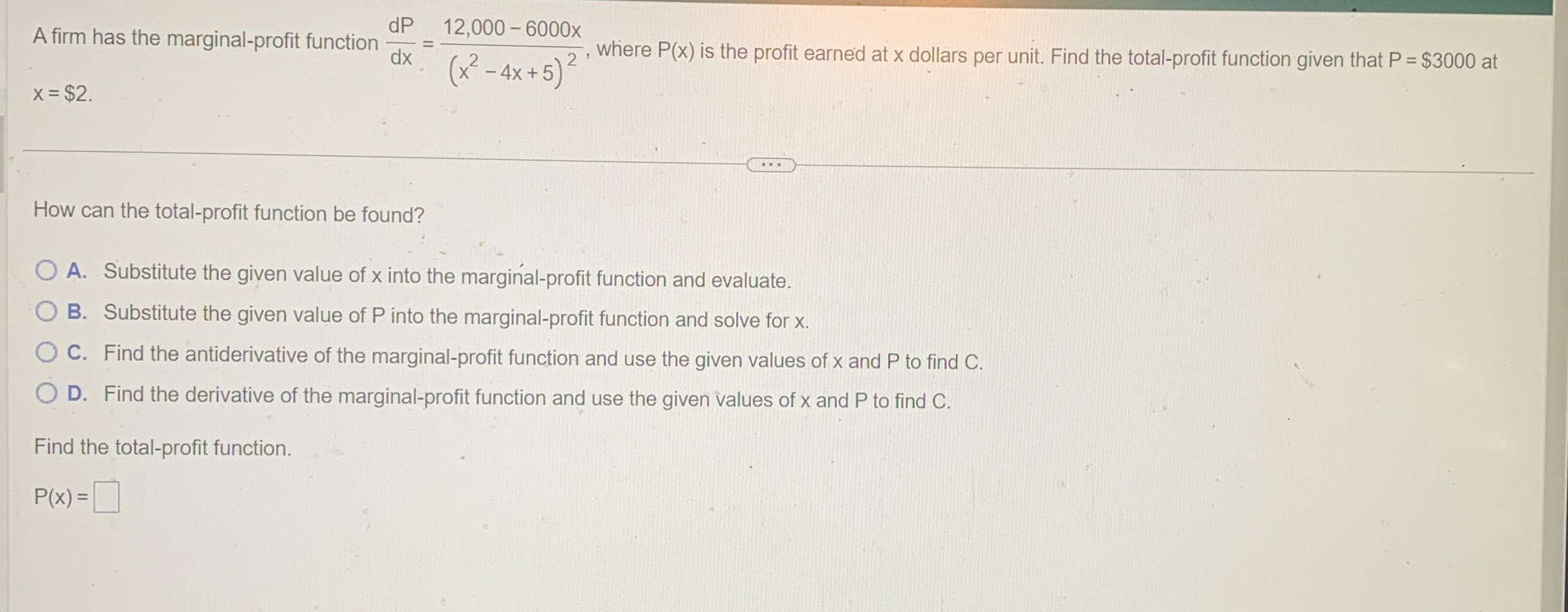
A firm has the marginal-profit function
(dP)/(dx)=(12,000-6000x)/((x^(2)-4x+5)^(2)), where
P(x)is the profit earned at
xdollars per unit. Find the total-profit function given that
P=$3000at
x=$2. How can the total-profit function be found? A. Substitute the given value of
xinto the marginal-profit function and evaluate. B. Substitute the given value of
Pinto the marginal-profit function and solve for
x. C. Find the antiderivative of the marginal-profit function and use the given values of
xand
Pto find
C. D. Find the derivative of the marginal-profit function and use the given values of
xand
Pto find
C. Find the total-profit function.
P(x)=
◻