(Solved): (a) Formulate a linear programming model that can be used to determine the percentage of the oak cab ...

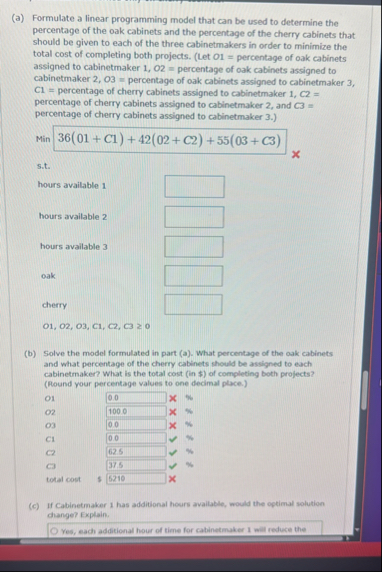
(a) Formulate a linear programming model that can be used to determine the percentage of the oak cabinets and the percentage of the cherry cabinets that should be given to each of the three cabinetmakers in order to minimize the total cost of completing both projects. (Let

percentage of oak cabinets assigned to cabinetmaker

percentage of oak cabinets assigned to cabinetmaker

percentage of oak cabinets assigned to cabinetmaker 3 , C1

percentage of cherry cabinets assigned to cabinetmaker

percentage of cherry cabinets assigned to cabinetmaker 2, and

percentage of cherry cabinets assigned to cabinetmaker 3.) Min s.t. hours available 1 hours available 2 hours available 3

oak

cherry

01, 02, 03, C1, C2, C3 : व (b) Solve the model formulated in part (a). What percentage of the oak cabinets and what percentage of the cherry cabinets should be assigned to each cabinetmaken? What is the total cost (in $) of completing both profects? (Round your percentage values to one decimal place.) O1

or

o3

Cl

C2

Cl

total cost s

(c) If Cabinetmaker 1 has additional hours available, would the optimal solution change? Explain. Yes, each additional hour of time for cabinetmater 1 wll reduce theC2

% C3

% total cost

(c) If Cabinetmaker 1 has additional hours available, would the optimal solution change? Explain. Yes, each additional hour of time for cabinetmaker 1 will reduce the total cost by $-1.75 per hour. Yes, each additional hour of time for cabinetmaker 1 will reduce the total cost by

per hour. No, cabinetmaker 1 has a slack of 26.458 hours, so increasing cabinetmaker 1's time will not reduce costs. No, cabinetmaker 1 has a slack of 37.5 hours, so increasing cabinetmaker 1 's time will not reduce costs. (d) If Cabinetmaker 2 has additional hours available, would the optimal solution change? Explain. Yes, each additional hour of time for cabinetmaker 2 will reduce the total cost by $-1.75 per hour. Yes, each additional hour of time for cabinetmaker 2 will reduce the total cost by

per hour. No, cabinetmaker 2 has a slack of 26.458 hours, so increasing cabinetmaker 2 's time will not reduce costs. No, cabinetmaker 2 has a slack of 37.5 hours, so increasing cabinetmaker 2's time will not reduce costs. (e) Suppose Cabinetmaker 2 reduced its cost to

per hour. What effect would this change have on the optimal solution? Explain. The new objective function coefficients for

and

are

and

respectively. The optimal solution

does not change

and has a value of $

-