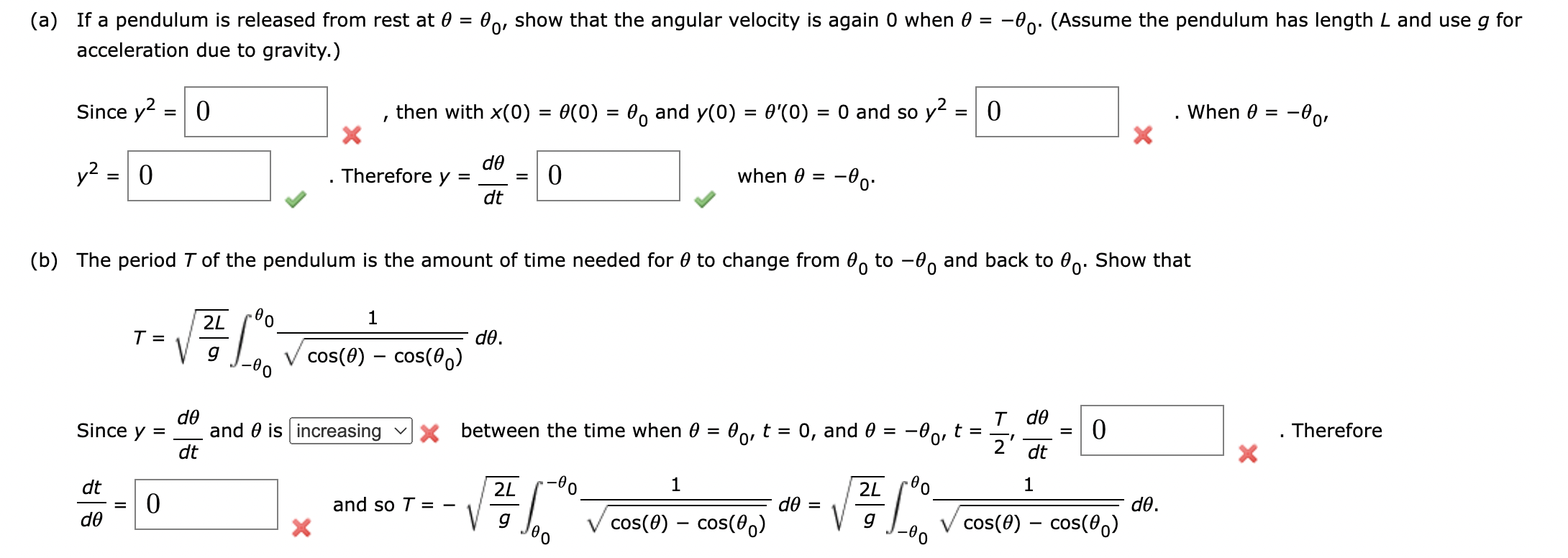(Solved): (a) If a pendulum is released from rest at \( \theta=\theta_{0} \), show that the angular velocity ...

(a) If a pendulum is released from rest at \( \theta=\theta_{0} \), show that the angular velocity is again 0 when \( \theta=-\theta_{0} \). (Assume the pendulum has length \( L \) and use \( g \) for acceleration due to gravity.) (b) The period \( T \) of the pendulum is the amount of time needed for \( \theta \) to change from \( \theta_{0} \) to \( -\theta_{0} \) and back to \( \theta_{0} \). Show that \[ T=\sqrt{\frac{2 L}{g}} \int_{-\theta_{0}}^{\theta_{0}} \frac{1}{\sqrt{\cos (\theta)-\cos \left(\theta_{0}\right)}} d \theta \] Since \( y=\frac{d \theta}{d t} \) and \( \theta \) is \( \quad \times \) between the time when \( \theta=\theta_{0}, t=0 \), and \( \theta=-\theta_{0}, t=\frac{T}{2}, \frac{d \theta}{d t}= \) Therefore \[ \frac{d t}{d \theta}=\quad \text { and so } T=-\sqrt{\frac{2 L}{g}} \int_{\theta_{0}}^{-\theta_{0}} \frac{1}{\sqrt{\cos (\theta)-\cos \left(\theta_{0}\right)}} d \theta=\sqrt{\frac{2 L}{g}} \int_{-\theta_{0}}^{\theta_{0}} \frac{1}{\sqrt{\cos (\theta)-\cos \left(\theta_{0}\right)}} d \theta \text {. } \]