Home /
Expert Answers /
Advanced Math /
a-researcher-selects-a-random-sample-of-138-college-students-from-her-local-university-for-each-stu-pa693
(Solved): A researcher selects a random sample of 138 college students from her local university. For each stu ...
A researcher selects a random sample of 138 college students from her local university. For each student, she records if they are full- or part-time and whether they sleep well. She would like to know if there is convincing evidence that school schedule is associated with sleeping. Let α = 0.05. The observed and expected counts are displayed in the tables. Observed counts: Schedule Expecte Full-Time Part-Time Sleep Well? Yes No 28 37 24 49 Which of the following contributed the most to the value of the x² statistic? O full-time student and sleeps well O part-time student and sleeps well O full-time student and does not sleep well O part-time student and does not sleep well
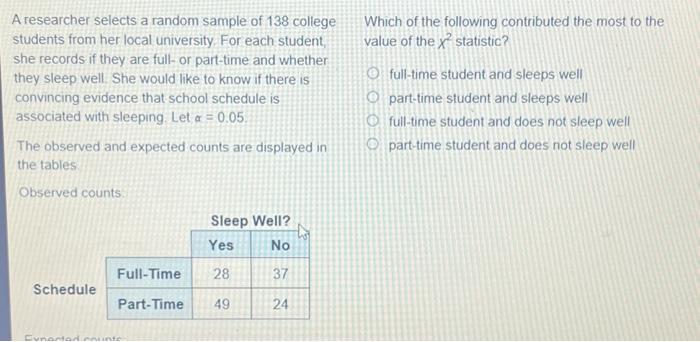
A researcher selects a random sample of 138 college Which of the following contributed the most to the students from her local university. For each student value of the statistic? she records if they are full- or part-time and whether they sleep well. She would like to know if there is full-time student and sleeps well convincing evidence that school schedule is part-time student and sleeps well associated with sleeping Let . full-time student and does not sleep well The observed and expected counts are displayed in part-time student and does not sleep well the tables observed counts Sched
Expert Answer
To determine which category contributed the most to the value of the chi-square statistic, we need to compare the observed and expected counts for each category and calculate the contribution for each.The chi-square statistic is calculated using the formula: Where: = observed count for category i = expected count for category iTo analyze the contribution of each category to the chi-square statistic, we compare the observed counts ( ) and expected counts ( ) for each category. By calculating the squared difference between the observed and expected counts, dividing it by the expected count, and summing these values for all categories, we obtain the chi-square statistic ( ).