(Solved): A solid steel shaft is supported by two bearings, points B and C, and is driven by a gear with a pri ...

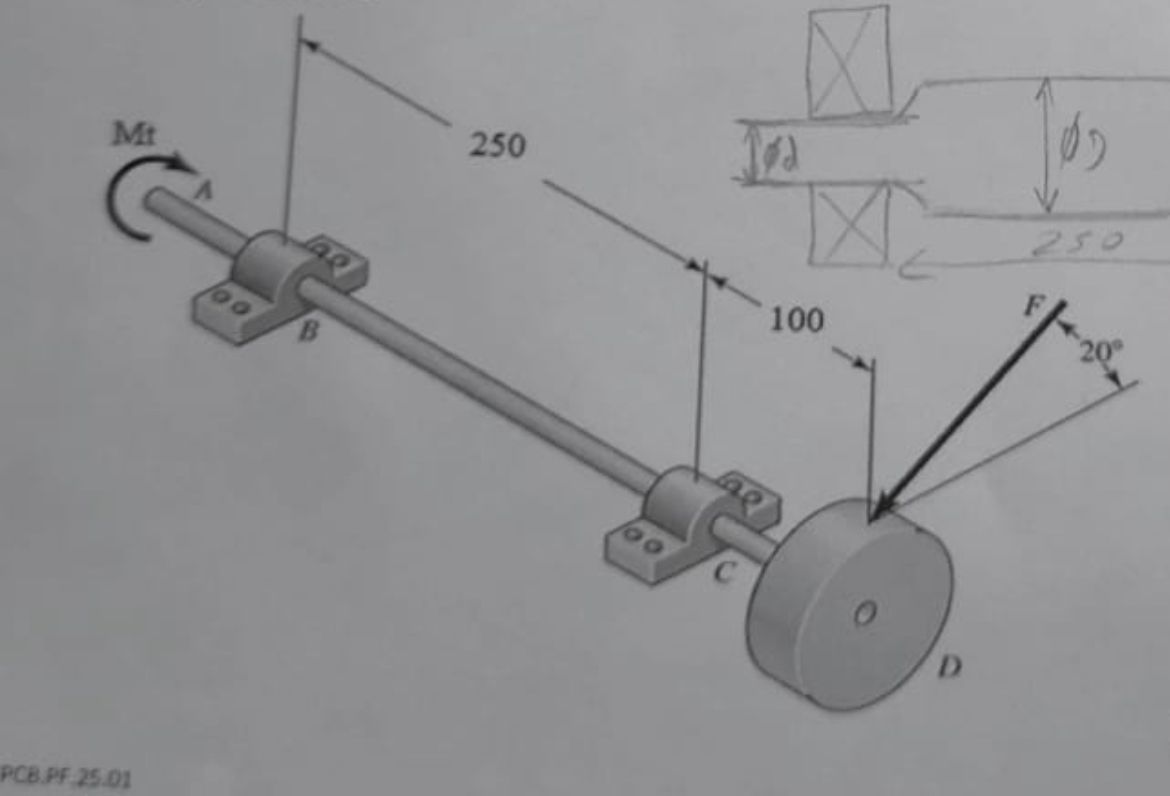
A solid steel shaft is supported by two bearings, points B and C, and is driven by a gear with a primitive diameter of 350 mm (gear D). The force applied by the gear at D acts at an angle of 20° relative to the vertical plane, transmitting a torque to point A of 800 Nm. The shaft is machined from steel with an ultimate tensile strength σc=520 MPa and yield strength σr=760 MPa. Assume that the support points B and C have a section variation with the following characteristics: D/d=1.5 and r/d=0.1. Using a safety factor of 1.75, assume the shaft operates at a temperature of 25°C and reliability of 95%. Determine: a) The minimum diameter of the shaft using the Soderberg criterion. b) Considering the geometry and dimensions of the shaft, select a key (Type A, NP standard) to allow the transmission of torque from gear D to the shaft. For the key selection, use a safety coefficient of 1.5, and assume it is made of DIN Ck45 K steel with σc=280 MPa. c) The critical frequencies due to lateral vibrations. For the calculation of transverse deformation, provide the formulation for integrating the elastic line. Assume the gear mass is 120 kg120 and E=200 GPa. PCB.PF 25.01