(Solved): A survey asked, "How many tattoos do you currently have on your body?" Of the 1229 males surveyed, ...

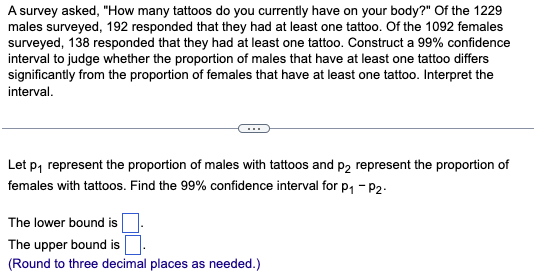
A survey asked, "How many tattoos do you currently have on your body?" Of the 1229 males surveyed, 192 responded that they had at least one tattoo. Of the 1092 females surveyed, 138 responded that they had at least one tattoo. Construct a \( 99 \% \) confidence interval to judge whether the proportion of males that have at least one tattoo differs significantly from the proportion of females that have at least one tattoo. Interpret the interval. Let \( p_{1} \) represent the proportion of males with tattoos and \( p_{2} \) represent the proportion of females with tattoos. Find the \( 99 \% \) confidence interval for \( p_{1}-p_{2} \). The lower bound is The upper bound is (Round to three decimal places as needed.) Interpret the interval. A. There is a 99\% probability that the difference of the proportions is in the interval. Conclude that there is insufficient evidence of a significant difference in the proportion of males and females that have at least one tattoo. B. There is \( 99 \% \) confidence that the difference of the proportions is in the interval. Conclude that there is a significant difference in the proportion of males and females that have at least one tattoo. C. There is a \( 99 \% \) probability that the difference of the proportions is in the interval. Conclude that there is a significant difference in the proportion of males and females that have at least one tattoo. D. There is \( 99 \% \) confidence that the difference of the proportions is in the interval. Conclude that there is insufficient evidence of a significant difference in the proportion of males and females that have at least one tattoo.