(Solved): A thin-walled container (vessel) made of steel of length 1 , outer diameter \( \mathrm{D} \) and i ...

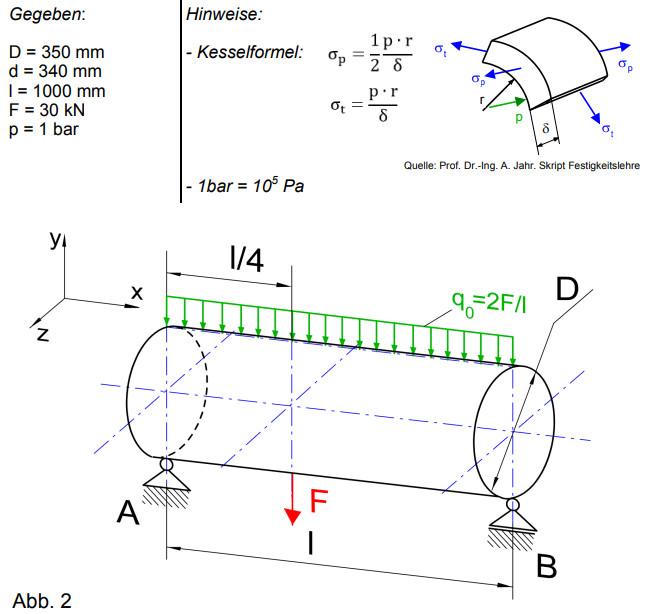
A thin-walled container (vessel) made of steel of length 1 , outer diameter \( \mathrm{D} \) and inner diameter \( \mathrm{d} \) (Fig. 2) is supported at points \( \mathrm{A} \) and \( \mathrm{B} \), as sketched. The container is with the distributed load \( \mathrm{q}_{0} \) (own weight) and loaded with a shear force \( \mathrm{F} \) as outlined. In addition, the pressure p prevails inside the container. a) State the location of the maximum stress on the container, justify your statement, b) b) determine the plane stress state at this point, c) c) determine the principal normal stresses \( \sigma 1 \) and \( \sigma 2 \), the mean normal stress ÿm and the maximum shear stress ÿmax (with the help of Mohr's stress circle, mathematically or graphically), d) graphically represent the associated section planes under their angle \( \varphi \) \[ \begin{array}{l|ll} \mathrm{D}=350 \mathrm{~mm} & -\text { Kesselformel: } & \sigma_{\mathrm{p}}=\frac{1}{2} \frac{\mathrm{p} \cdot \mathrm{r}}{\delta} \\ \mathrm{d}=340 \mathrm{~mm} & \sigma_{\mathrm{t}}=\frac{\mathrm{p} \cdot \mathrm{r}}{\delta} \\ \mathrm{l}=1000 \mathrm{~mm} \\ \mathrm{~F}=30 \mathrm{kN} & \\ \mathrm{p}=1 \mathrm{bar} & & \\ & & \\ & & \\ -1 \mathrm{bar}=10^{5} \mathrm{~Pa} & \end{array} \] TNN. \( \angle \)