(Solved): A uniform disk of mass m and radius r rolls without slip along the inside of a fixed circular track ...

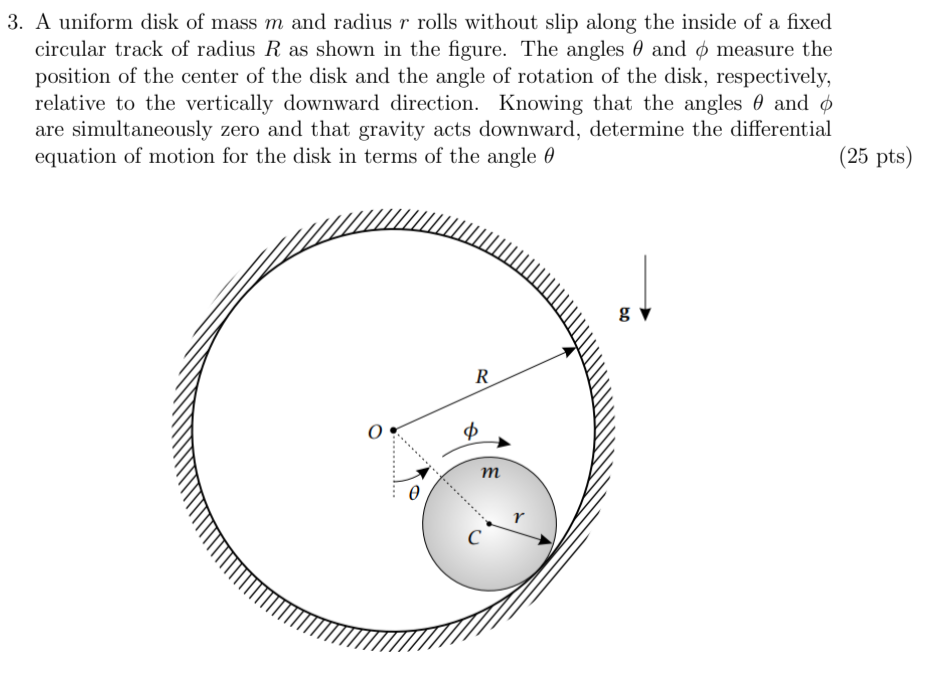
A uniform disk of mass m and radius r rolls without slip along the inside of a fixed circular track of radius R as shown in the figure. The angles θ and ϕ measure the position of the center of the disk and the angle of rotation of the disk, respectively, relative to the vertically downward direction. Knowing that the angles θ and ϕ are simultaneously zero and that gravity acts downward, determine the differential equation of motion for the disk in terms of the angle θ. Using Euler's Theorem by finding the angular momentum then finding d/dt of the angular momentum using transport theorem.