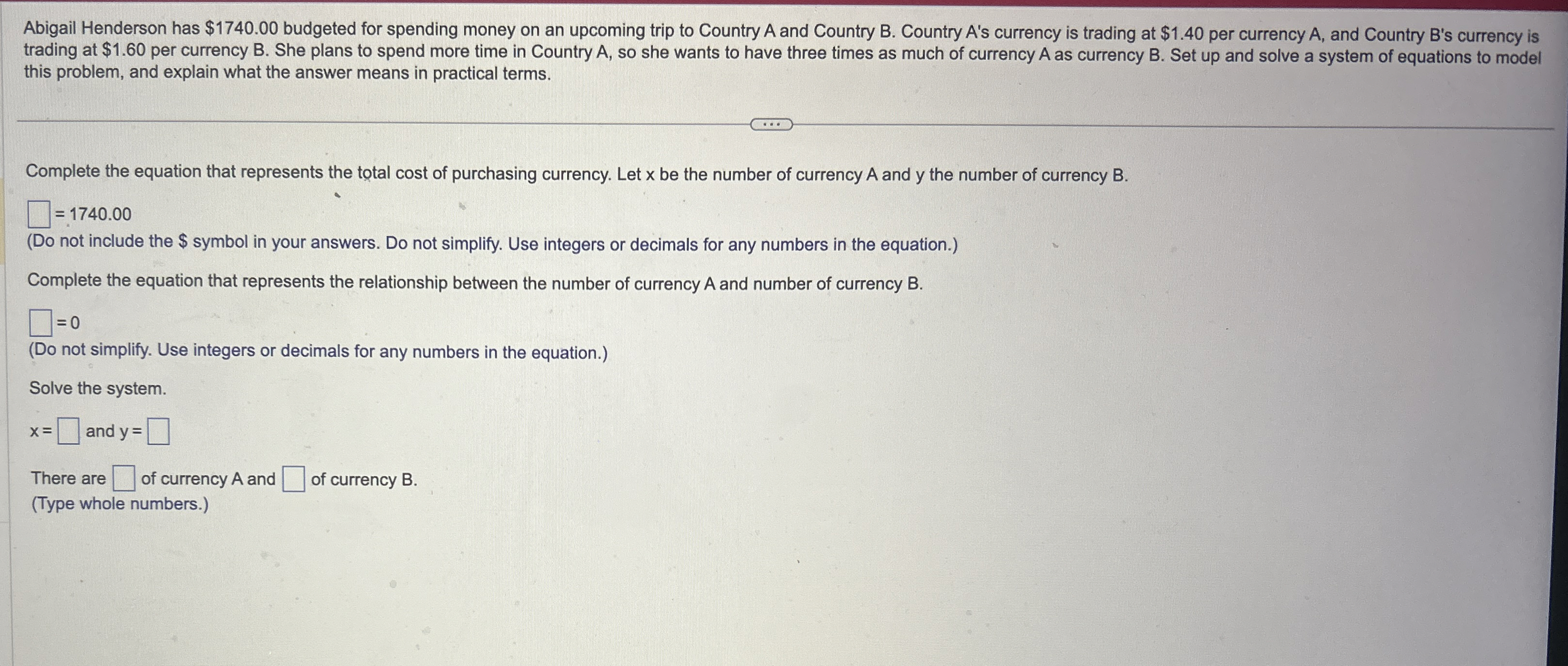
(Solved): Abigail Henderson has $1740.00 budgeted for spending money on an upcoming trip to Country A and Coun ...

Abigail Henderson has

budgeted for spending money on an upcoming trip to Country A and Country B. Country A's currency is trading at

per currency A, and Country B's currency is trading at

per currency B. She plans to spend more time in Country A, so she wants to have three times as much of currency A as currency B. Set up and solve a system of equations to model this problem, and explain what the answer means in practical terms. Complete the equation that represents the total cost of purchasing currency. Let x be the number of currency

and

the number of currency

.

(Do not include the

symbol in your answers. Do not simplify. Use integers or decimals for any numbers in the equation.) Complete the equation that represents the relationship between the number of currency

and number of currency

.

(Do not simplify. Use integers or decimals for any numbers in the equation.) Solve the system.

and

There are

of currency A and

of currency B . (Type whole numbers.)