(Solved): all of these problems are intermediate algebra. can anyone please help and do all of them pls!!? A p ...

A population numbers 13,000 organisms initially and grows by \( 8.3 \% \) each year. Suppose \( P \) represents population and \( t \) represents the number of years of growth. An exponential model for the population can be written in the form \( P=a b^{t} \), where \[ P= \] A population numbers 11,000 organisms initially and decreases by \( 3.3 \% \) each year. Suppose \( P \) represents population, and \( t \) the number of years of growth. 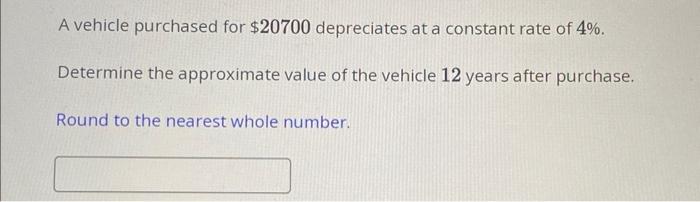An exponential model for the population can be written in the form \( P=a b^{t} \), where \[ P= \] A vehicle purchased for \( \$ 20700 \) depreciates at a constant rate of \( 4 \% \). Determine the approximate value of the vehicle 12 years after purchase. Round to the nearest whole number. A radioactive substance decays exponentially. A scientist begins with 160 milligrams of a radioactive substance. After 12 hours, 80 mg of the substance remains. How many milligrams will remain after 15 hours? \( \mathrm{mg} \) Give your answer accurate to at least one decimal place.