Home / Expert Answers / Civil Engineering / an-axial-bar-as-in-figure-1-with-span-b-is-made-of-material-with-modulus-of-elas-pa887

(Solved): An axial bar as in Figure 1 with span b is made of material with modulus of elas ...

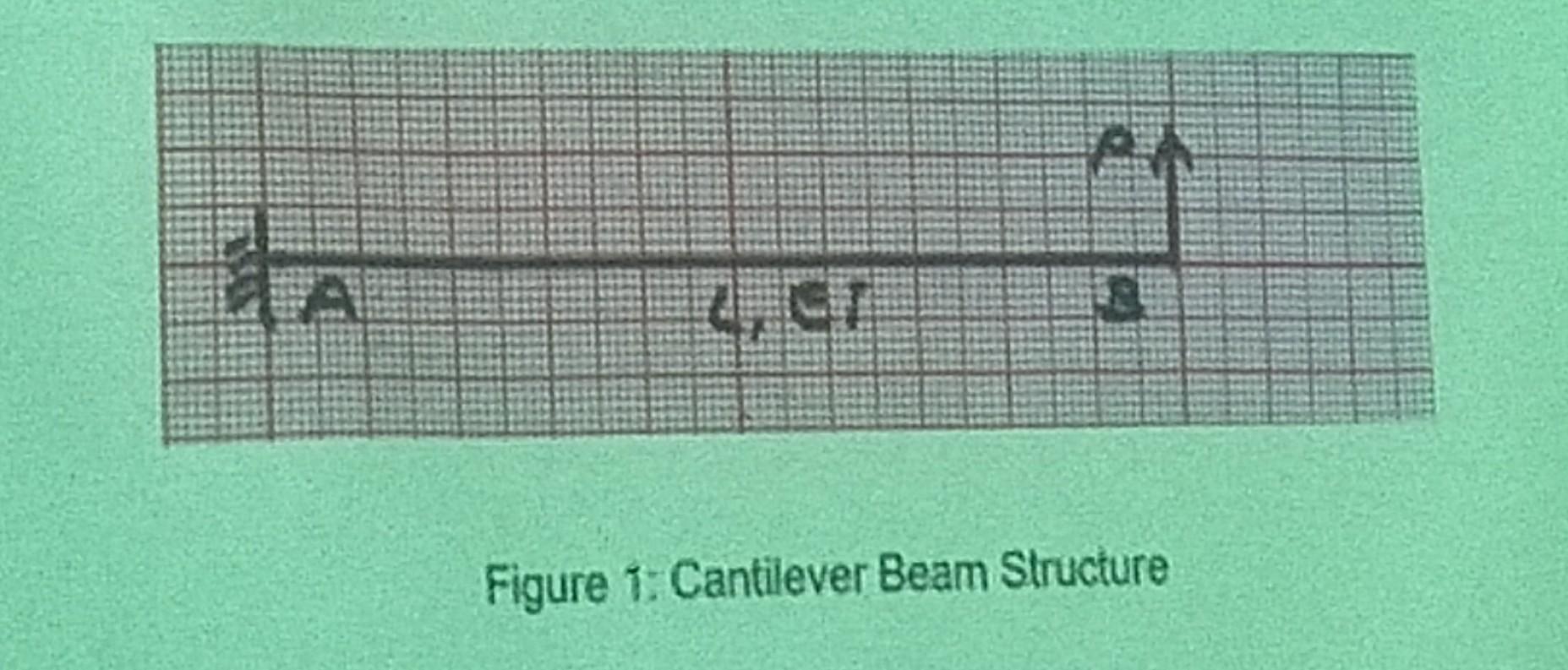
$An axial bar as in Figure 1 with span $ b $ is made of material with modulus of elasticity $ E $ and lineathy varied cros$

Figure 1: Cantilever Beam Structure

An axial bar as in Figure 1 with span

b

is made of material with modulus of elasticity

E

and lineathy varied cross section area given by

A (x) = (1 - x / L) A_{1} + (x / L) A_{2} = A_{1} + (Λ_{2} - A_{1})^{x}

in which

A_{1}

and

A_{2}

are the area of lett and right end sections respectively. The bar is modeled 83 one bar element with the two ends as nodes. Construct the stiffness matrix of the element. An axial bar as in Figure 1 with span

b

is made of material with modulus of elasticity

E

and lineathy varied cross section area given by

A (x) = (1 - x / L) A_{1} + (x / L) A_{2} = A_{1} + (Λ_{2} - A_{1})^{x}

in which

A_{1}

and

A_{2}

are the area of lett and right end sections respectively. The bar is modeled 83 one bar element with the two ends as nodes. Construct the stiffness matrix of the element. Figure 1: Cantilever Beam Structure

We have an Answer from Expert

View Expert Answer

Expert Answer

To construct the stiffness matrix of the element, we first need to derive the element stiffness matrix for an axial bar with a constant cross-sectional area. We can then modify this matrix to account for the linearly varying cross-sectional area

The element stiffness matrix for an axial bar with the constant cross-sectional area is given by


Where


Follow these steps as shows

We have an Answer from Expert

(Solved): An axial bar as in Figure 1 with span b is made of material with modulus of elas ...

View Expert Answer

Expert Answer

Buy This Answer $5

Place Order

We Provide Services Across The Globe