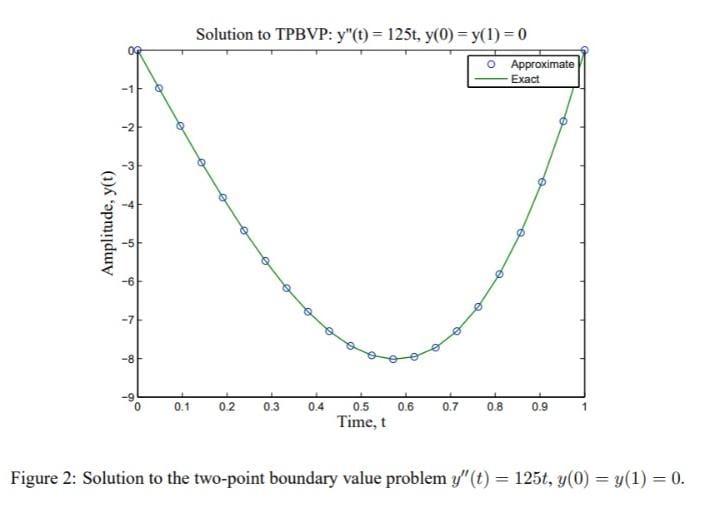
(Solved): Analytically find the exact solution to the two-point boundary value problem in y (t) y ...

Analytically find the exact solution to the two-point boundary value problem in y ??(t) ? y ? (t) = 125t, y(0) = y(1) = 0. On the same plot, display both the approximate values and the exact solution. Compare the approximations with the exact values at the grid points and Redo steps 1 and 2 when the boundary conditions are y(0) = 0 and y(1) = 1.

Help in converting so the grid points can be compared.

Solution for the two-point boundary problem(if it's correct):

%define all the symbols
syms x y(t)

%define and solve the quadratic equation for x
disp("actual equation is : ");
eqn = x^2-x-125
disp("Therefore,TValues of x are : ");
%print the answer
x=solve(eqn)

%define the ode
disp("Given : ")
diffEqn= diff(y,t,2) -diff(y,t) == 125*t
%define tboth the conditions
c1 = y(0) == 0;
c2 = y(1) == 0;
%make a vector of all the conditions
arr = [c1 c2];
%solve using dsolve()
y(t) = dsolve(diffEqn,arr);
disp("The value of y : ");
%simplify and print the answer
y = simplify(y)

 

G Solution to TPBVP:y"(t) = 125t, y(0) = y(1) = 0 O Approximate Exact -1 -2 D -3 -4 Amplitude, y(t) 0 -5 -6 ee -7 -8 -9 0 0.1 02 0.3 0.6 0.7 0.8 0.9 0.4 0.5 Time, t Figure 2: Solution to the two-point boundary value problem y(t) = 125t, y(0) = y(1) = 0.