(Solved): \[ \begin{array}{ll} n_{1}=9 & n_{2}=16 \\ \bar{x}_{1}=116 & \bar{x}_{2}=155 \\ s_{1}=22 & s_{2}=17 ...

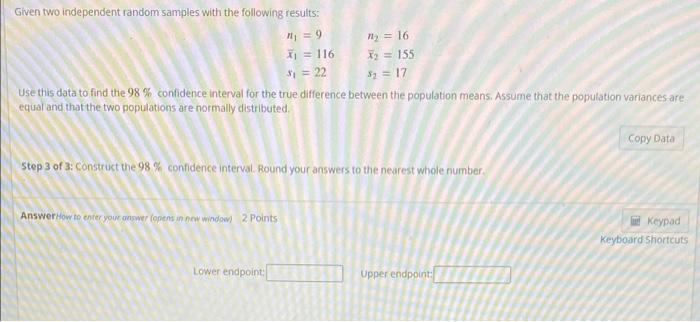
\[ \begin{array}{ll} n_{1}=9 & n_{2}=16 \\ \bar{x}_{1}=116 & \bar{x}_{2}=155 \\ s_{1}=22 & s_{2}=17 \end{array} \] Use this data to find the \( 98 \% \) confidence interval for the true difference between the population means. Assume that the population variances are equal and that the two populations are normally distributed. Step 1 of 3 : Find the point estimate that should be used in constructing the confidence interval. AnswerHow to enteryour antwer fasents in nnw window) 2 Polnts Keybonird Shorteuts Given two independent random samples with the following results: \[ \begin{array}{ll} n_{1}=9 & n_{2}=16 \\ \vec{x}_{1}=116 & \vec{x}_{2}=155 \\ s_{1}=22 & s_{2}=17 \end{array} \] Use this data to find the \( 98 \% \) confidence interval for the true difference between the population means. Assume that the population variances are equal and that the two populations are normally distributed. 5tep 3 of 3: Construct the \( 98 \% \) confidence interval. Round your answers to the nearest whole number. Answerthow to enter your onswer (opens in now window) 2 Points