Home /
Expert Answers /
Calculus /
c-where-is-g-x-0-enter-a-list-of-values-separated-by-commas-d-where-is-g-prime-pa463
(Solved): c) Where is \( g(x)=0 \) ? (Enter a list of values, separated by commas.) d) Where is \( g^{\prime} ...
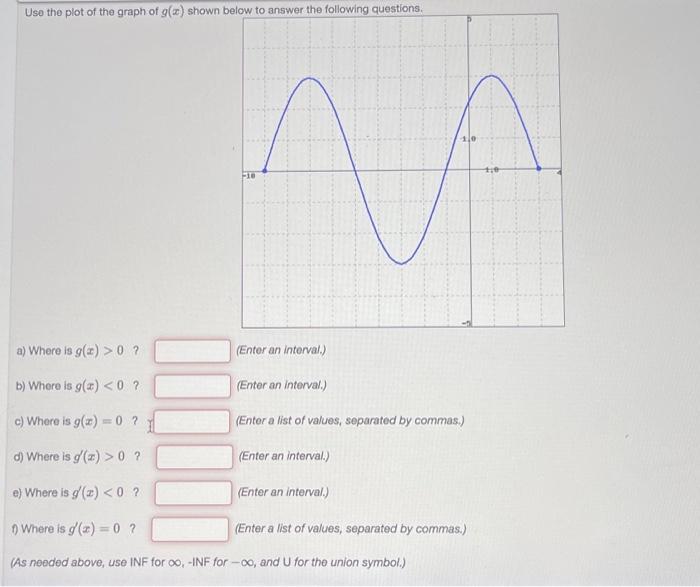
c) Where is \( g(x)=0 \) ? (Enter a list of values, separated by commas.) d) Where is \( g^{\prime}(x)>0 \) ? (Enter an interval.) e) Where is \( g^{\prime}(x)<0 \) ? (Enter an interval.) t) Where is \( g^{\prime}(x)=0 \) ? (Enter a list of values, separated by commas.) (As needed above, use INF for \( \infty \), -INF for \( -\infty \), and U for the union symbol.)
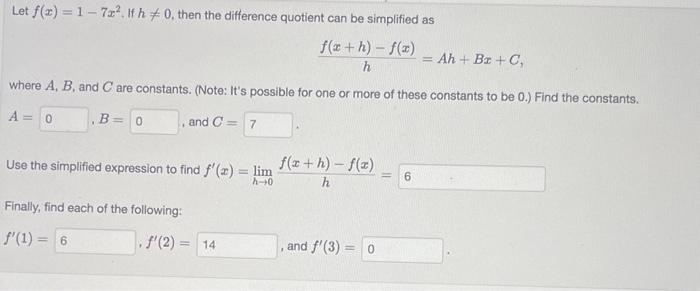
Let \( f(x)=1-7 x^{2} \). If \( h \neq 0 \), then the difference quotient can be simplified as \[ \frac{f(x+h)-f(x)}{h}=A h+B x+C, \] where \( A, B \), and \( C \) are constants. (Note: It's possible for one or more of these constants to be 0 .) Find the constants. \[ A=, B= \] Use the simplified expression to find \( f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}= \) Finally, find each of the following: \[ f^{\prime}(1)=, f^{\prime}(2)= \]
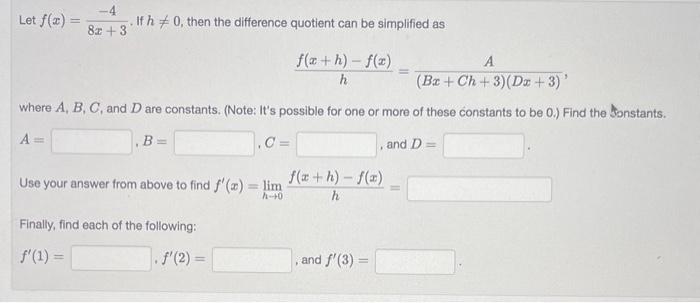
Let \( f(x)=\frac{-4}{8 x+3} \). If \( h \neq 0 \), then the difference quotient can be simplified as \[ \frac{f(x+h)-f(x)}{h}=\frac{A}{(B x+C h+3)(D x+3)} \] where \( A, B, C \), and \( D \) are constants. (Note: It's possible for one or more of these constants to be 0 .) Find the bonstants. \[ \begin{array}{l} A=B= \\ \text { Use your answer from above to find } f^{\prime}(x)=\lim _{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}= \end{array} \] Finally, find each of the following: \[ f^{\prime}(1)= \]
Expert Answer
1) a) g(x) > 0 = (-9,-5)U(