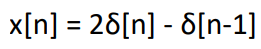(Solved): Calculate the discrete Fourier transforms of the signal shown below for N=2, 3 and 4. x[n]=2[n] ...

Expert Answer

---

To calculate the discrete Fourier transform (DFT) of the given signal x[n] = 2?[n] - ?[n-1] for different values of N, we'll use the formula:

X[k] = ? (x[n] * e^(-j2?kn/N)), where n ranges from 0 to N-1.

Let's calculate the DFT for N = 2, 3, and 4.

For N = 2:
X[0] = ? (x[n] * e^(-j2?kn/2)), where n ranges from 0 to 1.

Substituting the values of x[n] into the formula:
X[0] = (2 * e^(-j2?(0)(0)/2)) + (-1 * e^(-j2?(0)(1)/2))
= 2 * 1 + (-1 * 1)
= 2 - 1
= 1

X[1] = ? (x[n] * e^(-j2?kn/2)), where n ranges from 0 to 1.

Substituting the values of x[n] into the formula:
X[1] = (2 * e^(-j2?(1)(0)/2)) + (-1 * e^(-j2?(1)(1)/2))
= 2 * 1 + (-1 * 1)