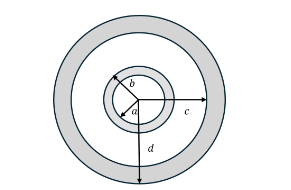
(Solved): .Consider a hollow sphere of nonzero thickness such that its inner surface has radius a while its ou ...

.Consider a hollow sphere of nonzero thickness such that its inner surface has radius a while its outer surface has radius b, and thus b > a. I take this sphere and completely surround it with another, hollow, but larger (concentric) sphere which also has nonzero thickness, with inner surface radius c and outer surface radius d (so, d > c). Note two important things: both spheres are made of metal and the space between the two spheres can be considered to be vacuum while the shaded regions are part of the sphere’s volume. The figure below illustrates the situation described in the question. The inner shell has total charge +Q, and the outer shell has charge +2Q. (a) By applying Gauss’s law, showing complete work and giving proper reason where applicable, determine the electric field (magnitude and direction) in the following regions of space: i. r < a, ii. a < r < b, iii . b< r < c, iv. c < r < d, v. r > d. Your answers should be in terms of fundamental constants, Q, r, and other fundamental constants. (b) Sketch a graph of E versus r, showing all of your results to (a) on a single set of axis. Clearly label the various regions on your sketch.