(Solved): Consider a system of two toy rail cars (i.e., frictionless masses). Suppose that car 1 has mass \( ...

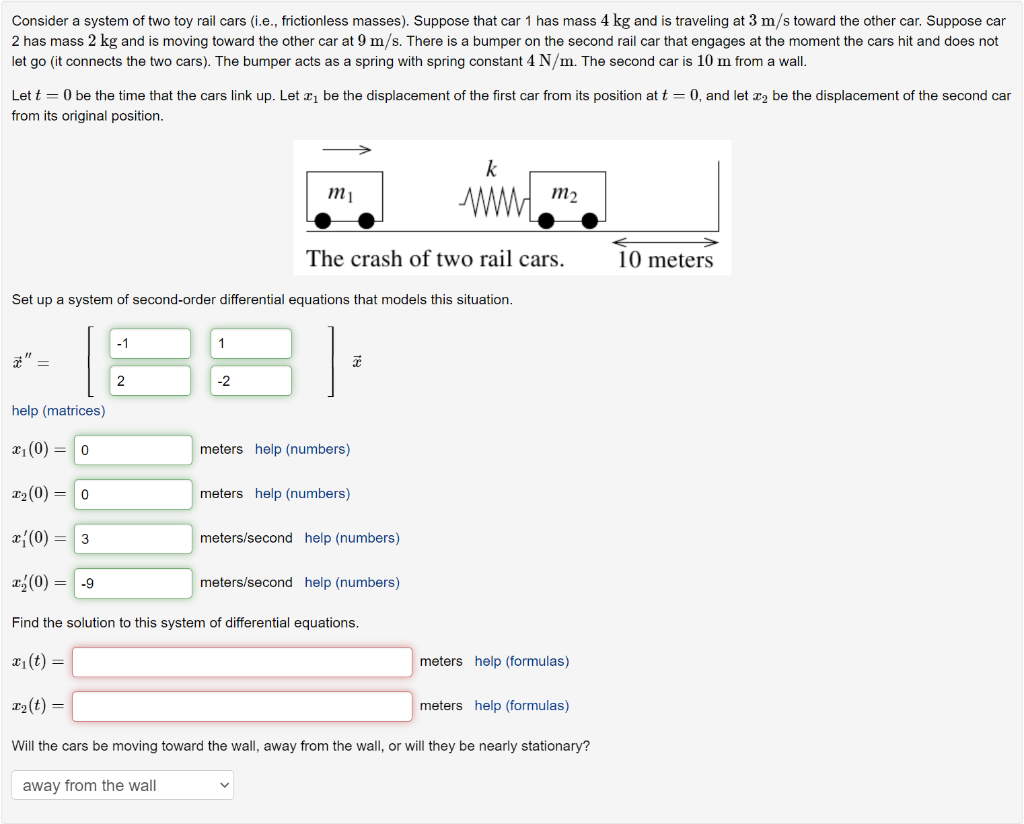
Consider a system of two toy rail cars (i.e., frictionless masses). Suppose that car 1 has mass \( 4 \mathrm{~kg} \) and is traveling at \( 3 \mathrm{~m} / \mathrm{s} \) toward the other car. Suppose car 2 has mass \( 2 \mathrm{~kg} \) and is moving toward the other car at \( 9 \mathrm{~m} / \mathrm{s} \). There is a bumper on the second rail car that engages at the moment the cars hit and does not let go (it connects the two cars). The bumper acts as a spring with spring constant \( 4 \mathrm{~N} / \mathrm{m} \). The second car is \( 10 \mathrm{~m} \) from a wall. Let \( t=0 \) be the time that the cars link up. Let \( x_{1} \) be the displacement of the first car from its position at \( t=0 \), and let \( x_{2} \) be the displacement of the second car from its original position. Set up a system of second-order differential equations that models this situation. Find the solution to this system of differential equations.