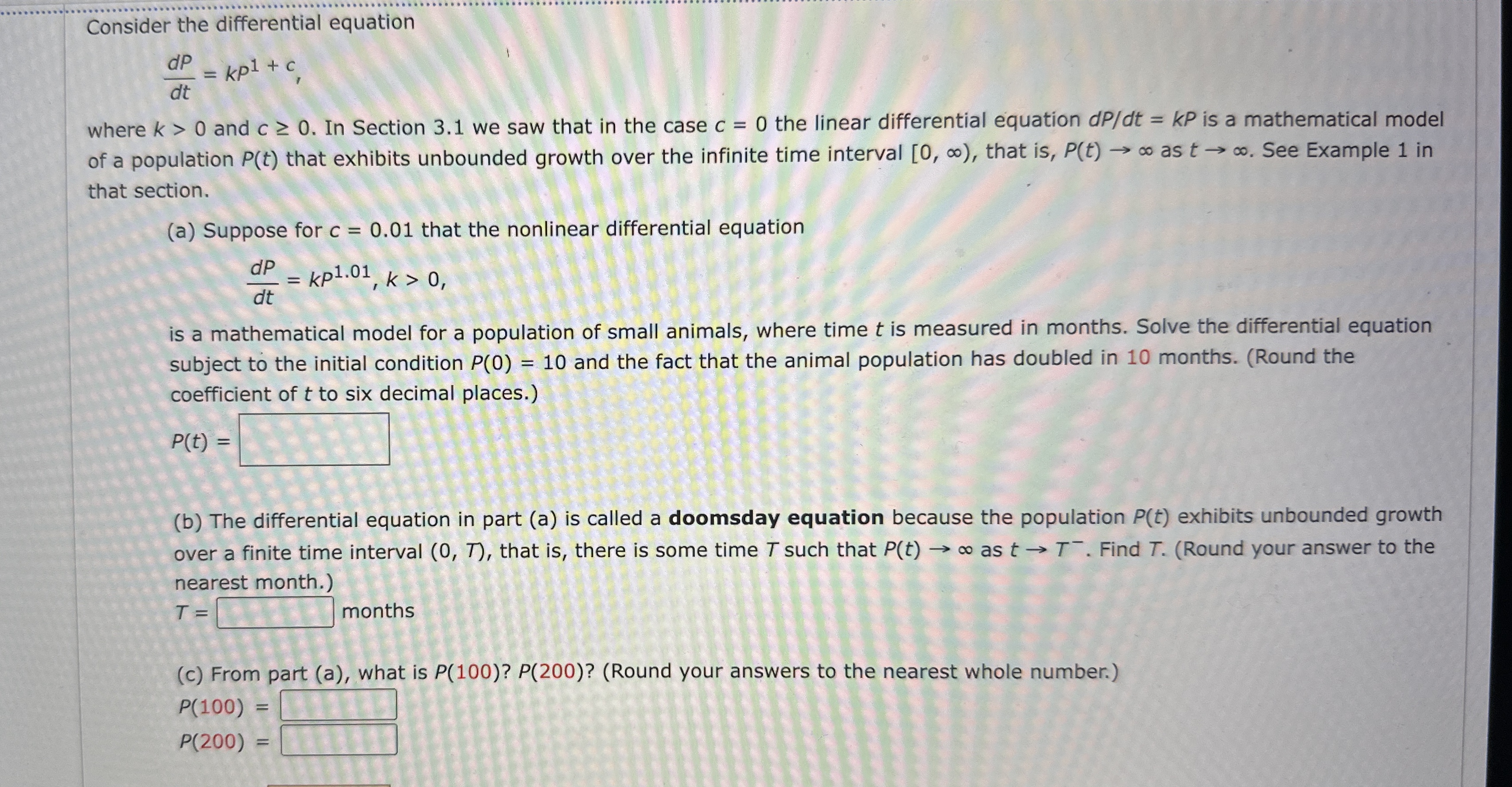
(Solved): Consider the differential equation (dP)/(dt)=kP^(1 c) where k>0 and c>=0. In Section 3.1 we sa ...
Consider the differential equation
(dP)/(dt)=kP^(1 c)where
k>0and
c>=0. In Section 3.1 we saw that in the case
c=0the linear differential equation
d(P)/(d)t=kPis a mathematical model of a population
P(t)that exhibits unbounded growth over the infinite time interval
[0,\infty ), that is,
P(t)->\infty as
t->\infty . See Example 1 in that section. (a) Suppose for
c=0.01that the nonlinear differential equation
(dP)/(dt)=kP^(1.01),k>0is a mathematical model for a population of small animals, where time
tis measured in months. Solve the differential equation subject to the initial condition
P(0)=10and the fact that the animal population has doubled in 10 months. (Round the coefficient of
tto six decimal places.)
P(t)=
◻(b) The differential equation in part (a) is called a doomsday equation because the population
P(t)exhibits unbounded growth over a finite time interval
(0,T), that is, there is some time
Tsuch that
P(t)->\infty as
t->T^(-). Find
T. (Round your answer to the nearest month.)
T=
◻months (c) From part (a), what is
P(100)?
P(200)? (Round your answers to the nearest whole number.)
P(100)=
P(200)=