Home /
Expert Answers /
Advanced Physics /
consider-the-following-2d-hexagonal-bravais-lattice-with-lattice-constant-a-the-primitive-lattice-v-pa225
(Solved): Consider the following 2D hexagonal Bravais lattice with lattice constant a. The primitive lattice v ...
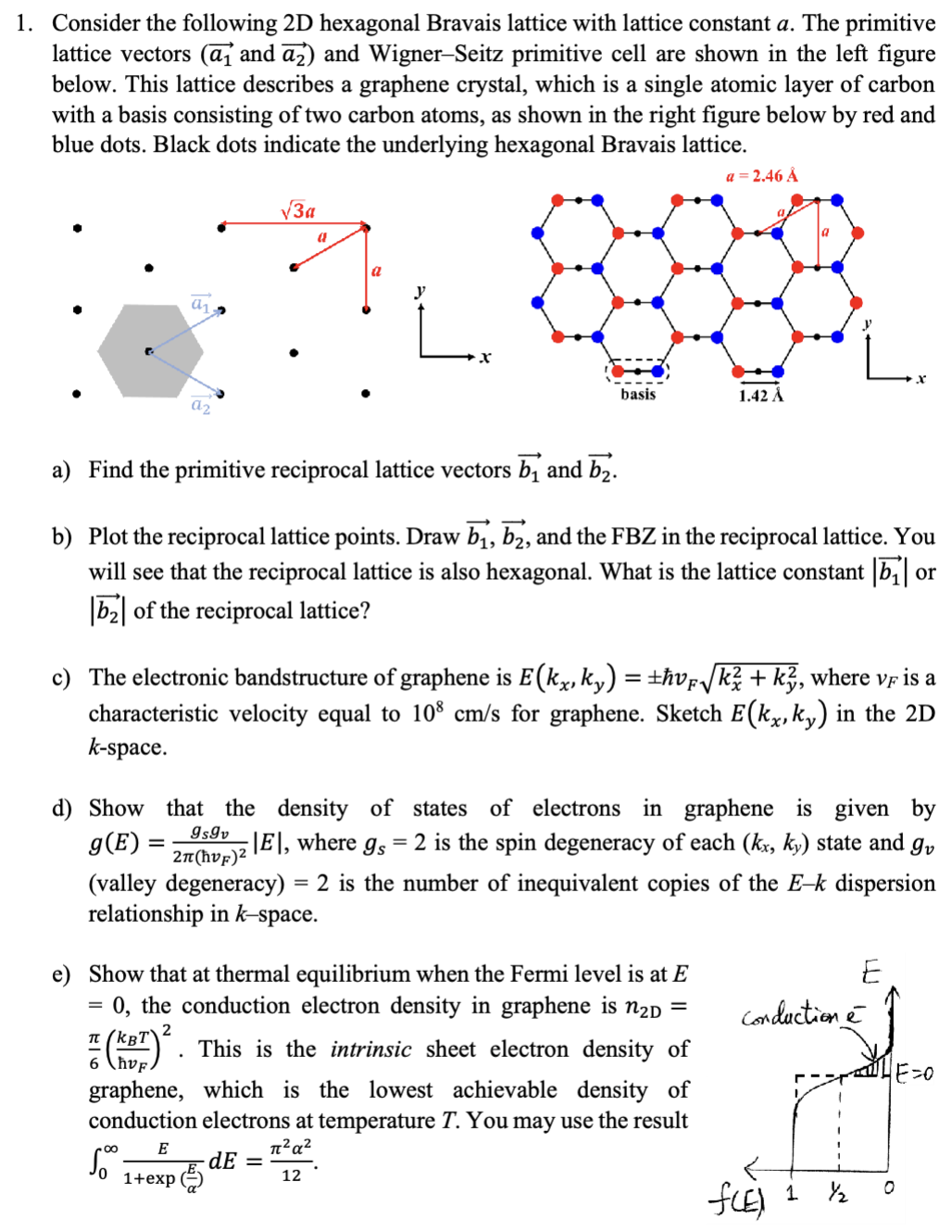
Consider the following 2D hexagonal Bravais lattice with lattice constant a. The primitive
lattice vectors and {:vec(a_(2))) and Wigner-Seitz primitive cell are shown in the left figure
below. This lattice describes a graphene crystal, which is a single atomic layer of carbon
with a basis consisting of two carbon atoms, as shown in the right figure below by red and
blue dots. Black dots indicate the underlying hexagonal Bravais lattice.
a=2.46\angstrom
avec(b_(1)) and vec(b_(2)).
bvec(b_(1)),vec(b_(2)), and the FBZ in the reciprocal lattice. You
will see that the reciprocal lattice is also hexagonal. What is the lattice constant |vec(b_(1))| or
|vec(b_(2))| of the reciprocal lattice?
cE(k_(x),k_(y))=+-ℏv_(F)\sqrt(k_(x)^(2)+k_(y)^(2)), where v_(F) is a
characteristic velocity equal to 10^(8)c(m)/(s) for graphene. Sketch E(k_(x),k_(y)) in the 2D
k-space.
dg(E)=(g_(s)g_(v))/(2\pi (ℏv_(F))^(2))|E|, where g_(s)=2 is the spin degeneracy of each (k_(x),k_(y)) state and g_(v)
(valley degeneracy) =2 is the number of inequivalent copies of the E-k dispersion
relationship in k-space.
eE
=0, the conduction electron density in graphene is n_(2D)=
(\pi )/(6)((k_(B)T)/(ℏv_(F)))^(2). This is the intrinsic sheet electron density of
graphene, which is the lowest achievable density of
conduction electrons at temperature T. You may use the result
\int_0^(\infty ) (E)/(1+exp((E)/(\alpha )))dE=(\pi ^(2)\alpha ^(2))/(12).