Home /
Expert Answers /
Chemical Engineering /
consider-the-following-2d-hexagonal-bravais-lattice-with-lattice-constant-avec-a-1-and-vec-a-2-pa720
(Solved): Consider the following 2D hexagonal Bravais lattice with lattice constant avec(a_(1)) and vec(a_(2)) ...
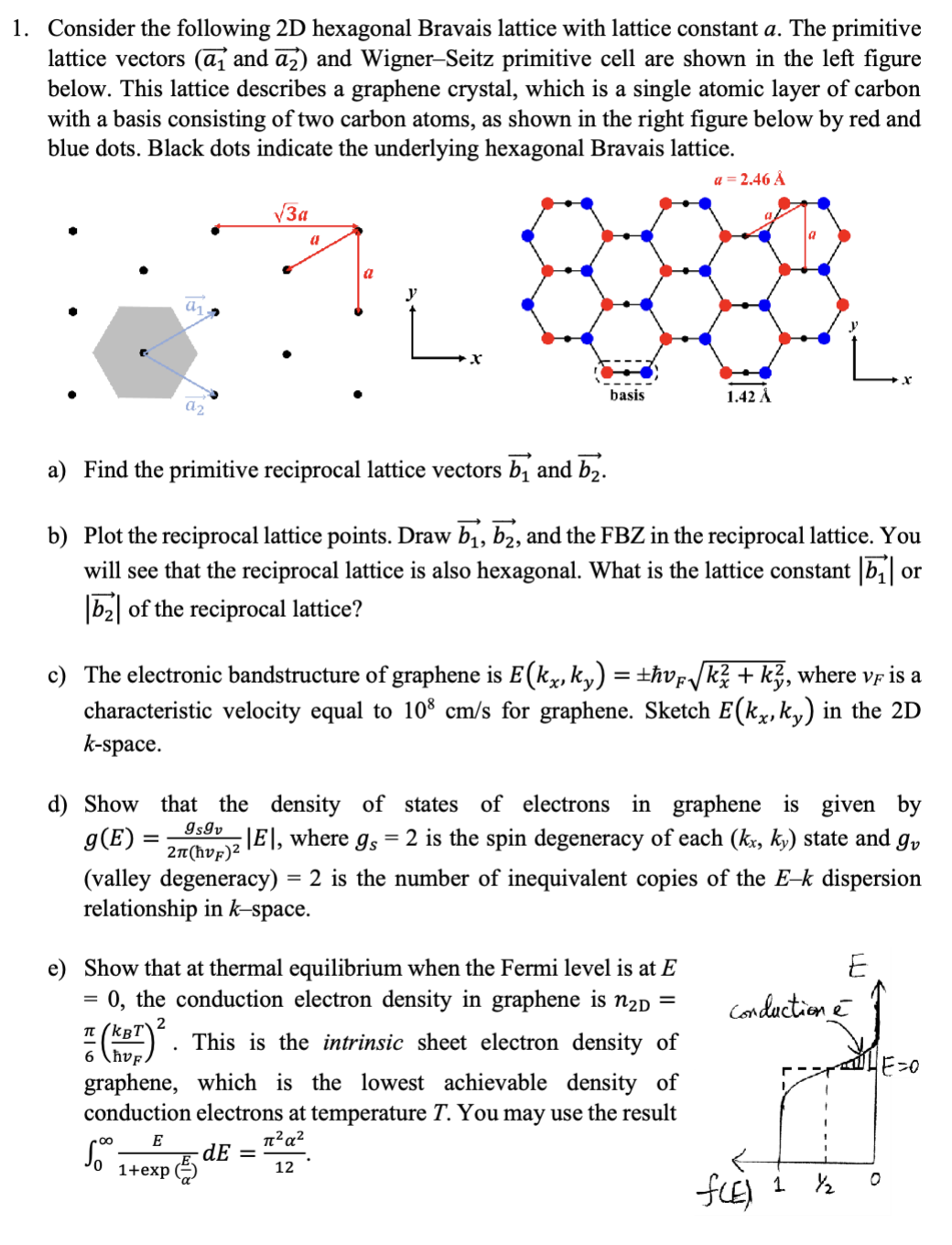
Consider the following 2D hexagonal Bravais lattice with lattice constant avec(a_(1)) and vec(a_(2)) vec(b_(1)) and vec(b_(2)).
bvec(b_(1)),vec(b_(2)), and the FBZ in the reciprocal lattice. You
will see that the reciprocal lattice is also hexagonal. What is the lattice constant |vec(b_(1))| or
|vec(b_(2))| of the reciprocal lattice?
cE(k_(x),k_(y))=+-ℏv_(F)\sqrt(k_(x)^(2)+k_(y)^(2)), where v_(F) is a
characteristic velocity equal to 10^(8)c(m)/(s) for graphene. Sketch E(k_(x),k_(y)) in the 2D
k-space.
dg(E)=(g_(s)g_(v))/(2\pi ((h)v_(F))^(2))|E|, where g_(s)=2 is the spin degeneracy of each (k_(x),k_(y)) state and g_(v)
(valley degeneracy) =2 is the number of inequivalent copies of the E-k dispersion
relationship in k-space.
eE
=0, the conduction electron density in graphene is n_(2D)=
(\pi )/(6)((k_(B)T)/(ℏv_(F)))^(2). This is the intrinsic sheet electron density of
graphene, which is the lowest achievable density of
conduction electrons at temperature T. You may use the result
\int_0^(\infty ) (E)/(1+exp((E)/(\alpha )))dE=(\pi ^(2)\alpha ^(2))/(12).