(Solved): Derive the open loop and close loop transfer function model of the Qube Servo 2 system and create a ...

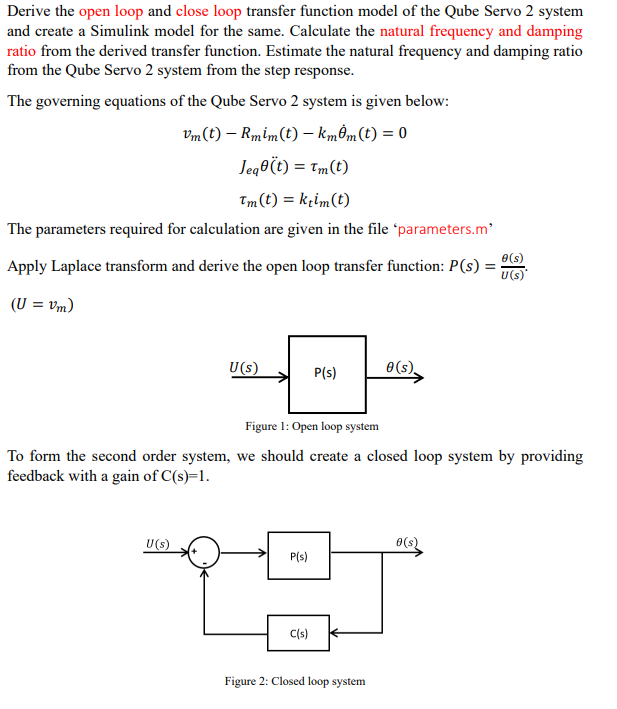
Derive the open loop and close loop transfer function model of the Qube Servo 2 system and create a Simulink model for the same. Calculate the natural frequency and damping ratio from the derived transfer function. Estimate the natural frequency and damping ratio from the Qube Servo 2 system from the step response. The governing equations of the Qube Servo 2 system is given below: $\begin{array}{c}{v}_m(t)-R_m{i}_m(t)-k_m{\dot{\theta }}_m(t)=0\\ J_{eq}\theta \ddot{\theta }t)={\tau }_m(t)\\ {\tau }_m(t)=k_t{i}_m(t)\end{array}$ The parameters required for calculation are given in the file 'parameters.m' Apply Laplace transform and derive the open loop transfer function: $P(s)=\frac{\theta (s)}{U(s)}$. $\left(U=v_m\right)$ To form the second order system, we should create a closed loop system by providing feedback with a gain of $\mathrm{C}(\mathrm{s})=1$. 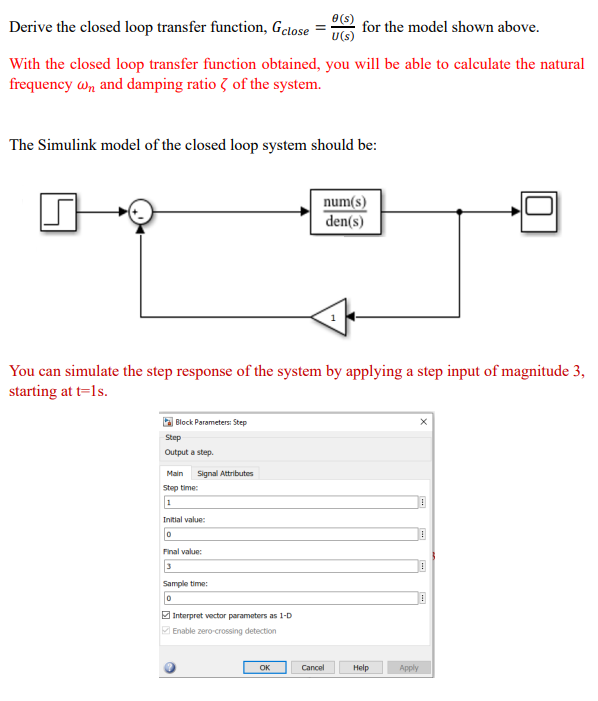Figure 2: Closed loop system Derive the closed loop transfer function, $G_{close}=\frac{\theta (s)}{U(s)}$ for the model shown above. With the closed loop transfer function obtained, you will be able to calculate the natural frequency ${\omega }_n$ and damping ratio $\zeta$ of the system. The Simulink model of the closed loop system should be: You can simulate the step response of the system by applying a step input of magnitude 3 , starting at $\mathrm{t}=1\mathrm{s}$. \% Resistance (ohm) $\mathrm{Rm}=8.4;$ $\%$ Inductance $(\mathrm{H})$ $\mathrm{Lm}=1.16\mathrm{e}-3$; \% Current-torque ( $\mathrm{N}$-m/A) $kt=0.042$; $\%$ Back-emf constant (V-s/rad) $\mathrm{km}=0.042$; $\%$ Rotor inertia $\left(\mathrm{kg}-{\mathrm{m}}^{\wedge }2\right)$ $Jr=4e-6;$ $\%$ Hub mass $(\mathrm{kg})$ $\mathrm{mh}=0.0106;\%9\mathrm{g}$ $\%$ Hub radius $(\mathrm{m})$ $\mathrm{rh}=22.2/1000/2;\%$ diameter $22.2\mathrm{mm}$ $\%$ Hub inertia $\left(\mathrm{kg}-{\mathrm{m}}^{\wedge }2\right)$ $\mathrm{Jh}=0.5\ast {\mathrm{mh}}^{\ast }{\mathrm{rh}}^{\wedge }2$; $\%$ Disc mass $(\mathrm{kg})$ $\mathrm{md}=0.053$; $\%$ Disc radius $(\mathrm{m})$ $rd=49.5/1000/2;\%$ diameter $=49.5\mathrm{mm}$ $\%$ Disc moment of inertia $\left(\mathrm{kg}-{\mathrm{m}}^{\wedge }2\right)$ $\mathrm{Jd}=0.5\ast {\mathrm{md}}^{\ast }{r}^{\wedge }2$; $\%$ Equivalent moment of inertia $\left(\mathrm{kg}-{\mathrm{m}}^{\wedge }2\right)$ $Jeq=Jr+Jh+Jd$;