Home /
Expert Answers /
Calculus /
determine-whether-the-following-series-converge-or-diverge-be-sure-to-mame-any-test-s-used-as-well-pa437
(Solved): Determine whether the following series converge or diverge- Be sure to mame any test(s) used as well ...
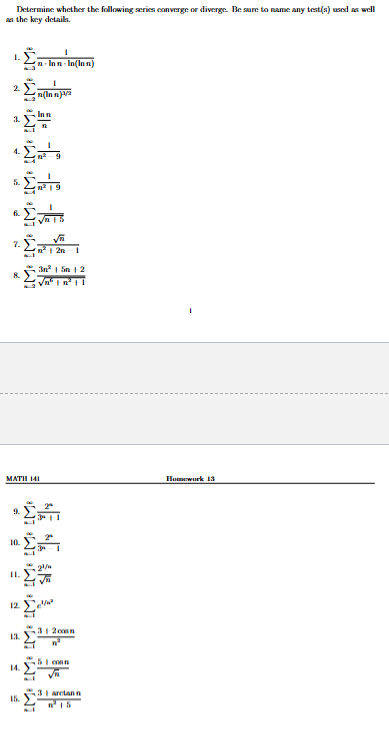
Determine whether the following series converge or diverge- Be sure to mame any test(s) used as well
as the key details.
\sum_(n=3)^(\infty ) (1)/(n*lnn*ln(lnn))
\sum_(n=2)^(\infty ) (1)/(n(lnn)^((1)/(2)))
a. \sum_(n=1)^(\infty ) (lnn)/(n)
\sum_(n=4)^(\infty ) (1)/(n^(2)-9)
\sum_(n=4)^(\infty ) (1)/(n^(2)+9)
\sum_(n=1)^(\infty ) (1)/(\sqrt(n+5))
\sum_(n=1)^(\infty ) (\sqrt(n))/(n^(2)+2n-1)
\sum_(n=2)^(\infty ) (3n^(2)+5n+2)/(\sqrt(n^(6)+n^(2)+1))
\sum_(n=1)^(\infty ) (2^(n))/(3^(n)+1)
\sum_(n=1)^(\infty ) (2^(n))/(3^(n)-1)
\sum_(n=1)^(\infty ) (2^((1)/(n)))/(\sqrt(n))
\sum_(n=1)^(\infty ) e^((1)/(n^(2)))
\sum_(n=1)^(\infty ) (3+2cosn)/(n^(2))
\sum_(n=1)^(\infty ) (5+cosn)/(\sqrt(n))
\sum_(n=1)^(\infty ) (3+arctann)/(n^(2)+5)