(Solved): Determine whether the following series converges. Justify your answer. \sum_(k=1)^(\infty ) (12k^(2) ...

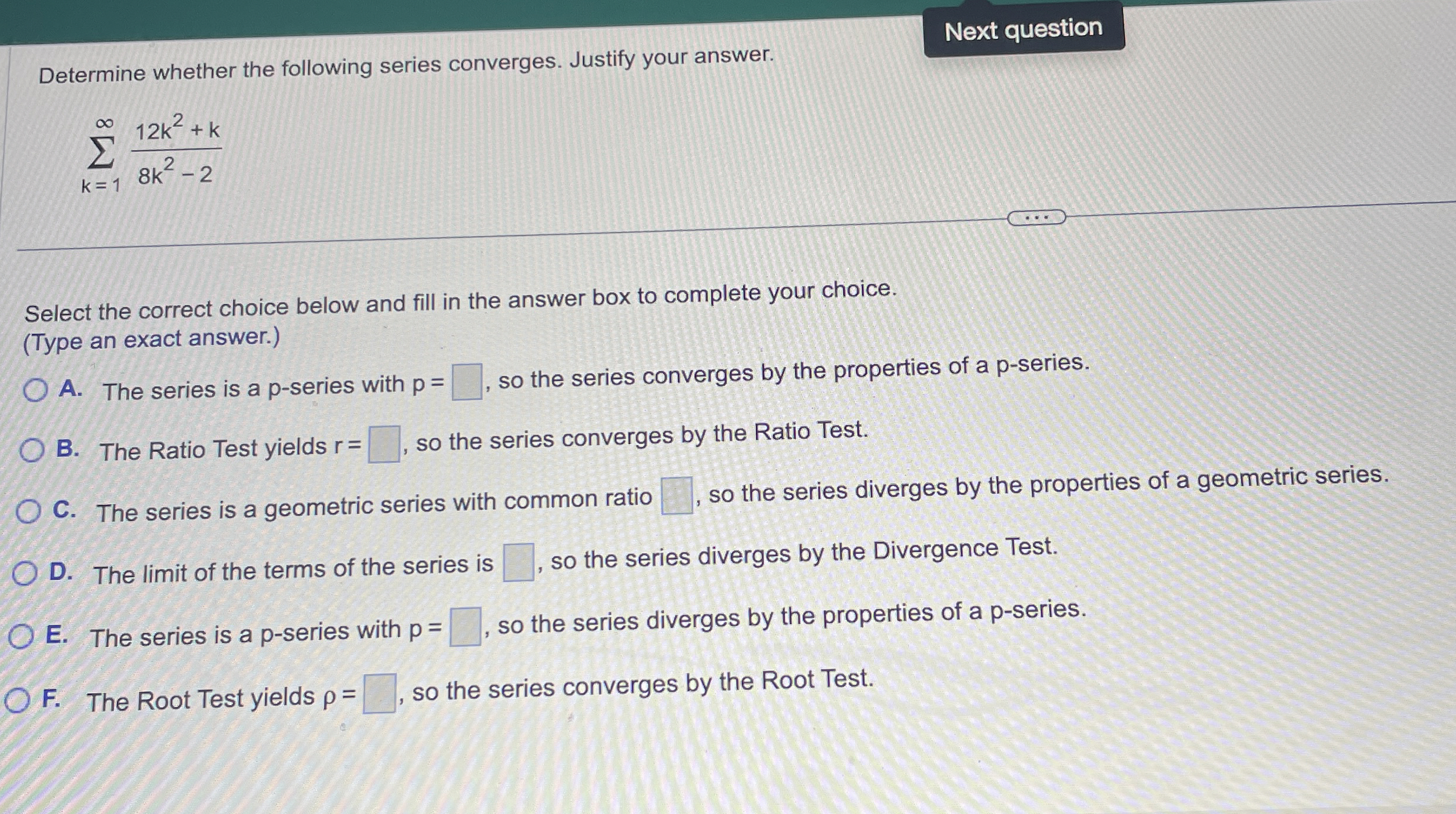
Determine whether the following series converges. Justify your answer.

Select the correct choice below and fill in the answer box to complete your choice. (Type an exact answer.) A. The series is a

-series with

so the series converges by the properties of a p-series. B. The Ratio Test yields

so the series converges by the Ratio Test. C. The series is a geometric series with common ratio

, so the series diverges by the properties of a geometric series. D. The limit of the terms of the series is

, so the series diverges by the Divergence Test. E. The series is a

-series with

so the series diverges by the properties of a p-series. F. The Root Test yields

, so the series converges by the Root Test.