(Solved): Do the following with the given information. \int_0^1 27cos(x^(2))dx (a) Find the approximations T_( ...
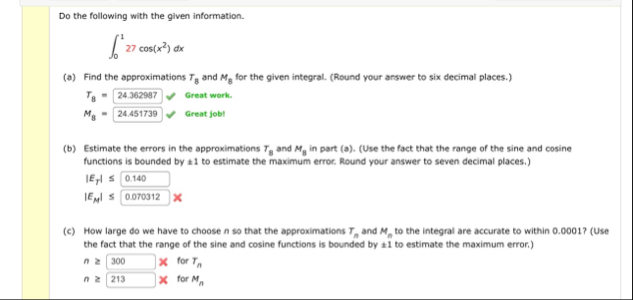
Do the following with the given information.
\int_0^1 27cos(x^(2))dx(a) Find the approximations
T_(8)and
M_(8)for the given integral. (Round your answer to six decimal places.)
T_(8)=,✓ Great work.
M_(8)=,✓ Great jobt (b) Estimate the errors in the approximations
T_(8)and
M_(8)in part (a). (Use the fact that the range of the sine and cosine functions is bounded by
!=1to estimate the maximum error. Round your answer to seven decimal places.)
|E_(T)|<=
|E_(M)|<=
q,
q,(c) How large do we have to choose
nso that the approximations
T_(n)and
M_(n)to the integral are accurate to within 0.0001 ? (Use the fact that the range of the sine and cosine functions is bounded by
-1to estimate the maximum error.)
n>=
q,
\times for
T_(n)
n>=
◻
\times for
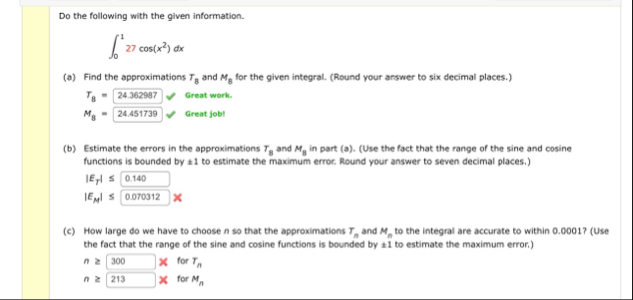
M_(n)Do the following with the given information.
\int_0^1 27cos(x^(2))dx(a) Find the approximations
T_(8)and
M_(8)for the given integral. (Round your answer to six decimal places.)
T_(8)=,✓ Great work.
M_(8)=,✓ Great jobt (b) Estimate the errors in the approximations
T_(8)and
M_(8)in part (a). (Use the fact that the range of the sine and cosine functions is bounded by
!=1to estimate the maximum error. Round your answer to seven decimal places.)
|E_(T)|<=
|E_(M)|<=
q,
q,(c) How large do we have to choose
nso that the approximations
T_(n)and
M_(n)to the integral are accurate to within 0.0001 ? (Use the fact that the range of the sine and cosine functions is bounded by
-1to estimate the maximum error.)
n>=
q,
\times for
T_(n)
n>=
◻
\times for
M_(n)