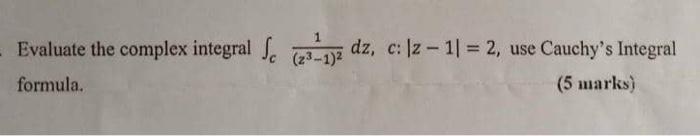Home / Expert Answers / Advanced Math / evaluate-the-complex-integral-int-c-frac-1-left-z-3-1-right-2-d-z-c-z-1-2-use-pa908

(Solved): Evaluate the complex integral \( \int_{c} \frac{1}{\left(z^{3}-1\right)^{2}} d z, c:|z-1|=2 \), use ...



Evaluate the complex integral \( \int_{c} \frac{1}{\left(z^{3}-1\right)^{2}} d z, c:|z-1|=2 \), use Cauchys Integral formula
Evaluate the complex integral \( \int_{c} \frac{1}{\left(z^{3}-1\right)^{2}} d z, c:|z-1|=2 \), use Cauchy's Integral formula. (5 marks)


We have an Answer from Expert

View Expert Answer

Expert Answer

The given complex integral is ?c1(z3?1)2dz,c:?z?1?=2 Poles of the function is (z3?1)2=0?(z3?1)=0?z3=1 Then roots of z are 1,w,w2 Where w=?1+32,w2=?1?3
We have an Answer from Expert

Buy This Answer $5

Place Order

We Provide Services Across The Globe

Order Now
Go To Answered Questions