(Solved): Figure 1: Nonlinear mass-spring-damper system The variables x1(t) and x2(t) represent the po ...

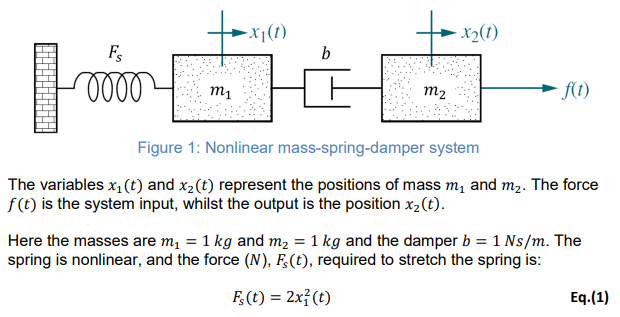
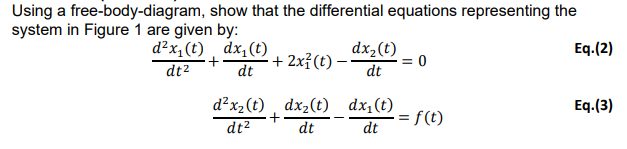
Figure 1: Nonlinear mass-spring-damper system The variables $x_1(t)$ and $x_2(t)$ represent the positions of mass $m_1$ and $m_2$. The force $f(t)$ is the system input, whilst the output is the position $x_2(t)$. Here the masses are $m_1=1\mathrm{kg}$ and $m_2=1\mathrm{kg}$ and the damper $b=1\mathrm{Ns}/\mathrm{m}$. The spring is nonlinear, and the force $(N),F_s(t)$, required to stretch the spring is: $F_S(t)=2x_1^2(t)$ Using a free-body-diagram, show that the differential equations representing the system in Figure 1 are given by: $\begin{array}{rl}\frac{d^2{x}_1(t)}{d{t}^2}+\frac{d{x}_1(t)}{dt}+2x_1^2(t)-\frac{d{x}_2(t)}{dt}& =0\\ \frac{d^2{x}_2(t)}{d{t}^2}+\frac{d{x}_2(t)}{dt}-\frac{d{x}_1(t)}{dt}& =f(t)\end{array}$