(Solved): Figure 1 shows the speed (mph) against time (s) graph of a vehicle in motion, starting at t=1, wher ...

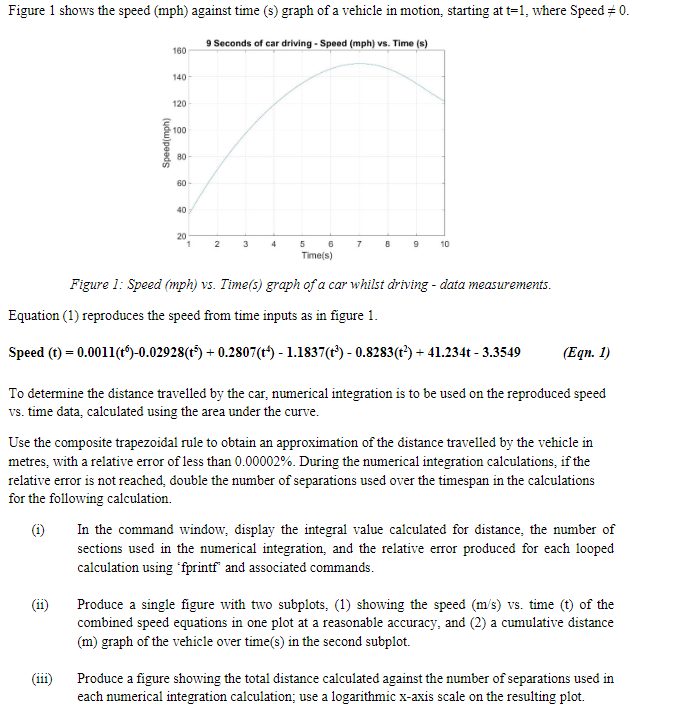
Figure 1 shows the speed (mph) against time (s) graph of a vehicle in motion, starting at t=1, where Speed != 0. Figure 1 shows the speed ) against time ( s Figure 1: Speed (mph) vs. Time(s) graph of a car whilst driving - data measurements. Equation (1) reproduces the speed from time inputs as in figure 1. Speed (t) = 0.0011(t6)-0.02928(t5) + 0.2807(t4) - 1.1837(t3) - 0.8283(t2) + 41.234t - 3.3549 (Eqn. 1) To determine the distance travelled by the car, numerical integration is to be used on the reproduced speed vs. time data, calculated using the area under the curve. Use the composite trapezoidal rule to obtain an approximation of the distance travelled by the vehicle in metres, with a relative error of less than 0.00002%. During the numerical integration calculations, if the relative error is not reached, double the number of separations used over the timespan in the calculations for the following calculation. (i) In the command window, display the integral value calculated for distance, the number of sections used in the numerical integration, and the relative error produced for each looped calculation using ‘fprintf’ and associated commands. (ii) Produce a single figure with two subplots, (1) showing the speed (m/s) vs. time (t) of the combined speed equations in one plot at a reasonable accuracy, and (2) a cumulative distance (m) graph of the vehicle over time(s) in the second subplot. (iii) Produce a figure showing the total distance calculated against the number of separations used in each numerical integration calculation; use a logarithmic x-axis scale on the resulting plot |||||||||||||||||| COULD YOU PLEASE EXPLAIN STEP BY STEP HOW IT SHOULD BE DONE USNING composite trapezoida RULES. PLEASE SHOW THE MATLAB CODE.