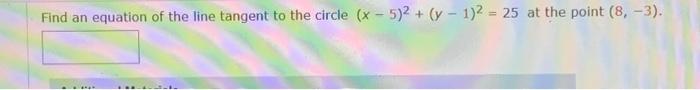Home / Expert Answers / Calculus / find-an-equation-of-the-line-tangent-to-the-circle-x5-2-y1-2-25-at-the-point-8-3-pa865

(Solved): Find an equation of the line tangent to the circle (x5)2+(y1)2=25 at the point (8,3). ...



Find an equation of the line tangent to the circle \( (x-5)^{2}+(y-1)^{2}=25 \) at the point \( (8,-3) \).
Find an equation of the line tangent to the circle at the point .


We have an Answer from Expert

View Expert Answer

Expert Answer


Solution: -

To find an equation of the line tangent to the circle at the point   , we need to determine the slope of the tangent line at that point.
The equation of the circle is given by:   
We can rewrite this equation in the standard form of a circle:   
Comparing this equation with the standard form:   
We can see that the center of the circle is at    and the radius is   .

We have an Answer from Expert

Buy This Answer $5

Place Order

We Provide Services Across The Globe

Order Now
Go To Answered Questions