Home /
Expert Answers /
Precalculus /
find-f-g-f-g-f-g-and-f-g-and-give-the-domain-of-each-new-function-if-an-answer-pa870
(Solved): Find \( f+g, f-g, f+g \), and \( f / g \), and give the domain of each new function. (If an answer ...
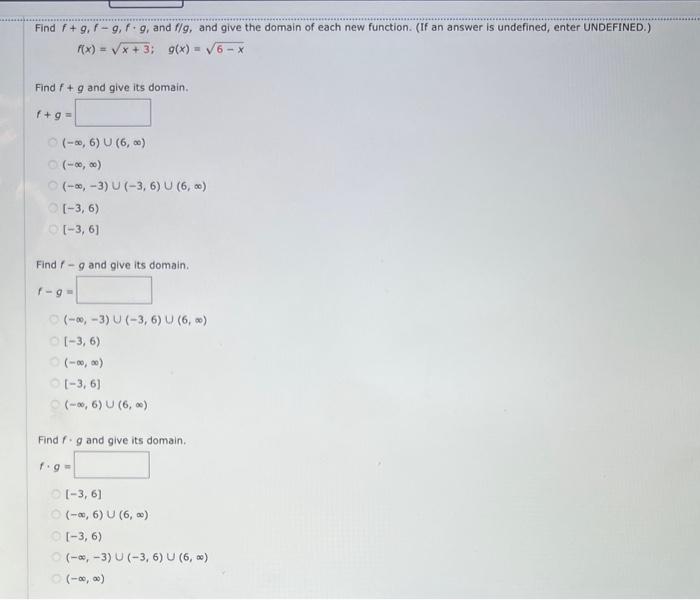
Find \( f+g, f-g, f+g \), and \( f / g \), and give the domain of each new function. (If an answer is undefined, enter UNDEFINED.) \[ f(x)=\sqrt{x+3} ; \quad g(x)=\sqrt{6-x} \] Find \( f+g \) and give its domain. \[ \begin{aligned} f+g & = \\ & (-\infty, 6) \cup(6, \infty) \\ & (-\infty, \infty) \\ & (-\infty,-3) \cup(-3,6) \cup(6, \infty) \\ & {[-3,6) } \\ & {[-3,6] } \end{aligned} \] Find \( f-g \) and give its domain. \[ \begin{aligned} f-g & \\ & (-\infty,-3) \cup(-3,6) \cup(6, \infty) \\ & {[-3,6) } \\ & (-\infty, \infty) \\ & {[-3,6] } \\ & (-\infty, 6) \cup(6, \infty) \end{aligned} \] Find \( f \cdot g \) and give its domain. \[ \begin{aligned} f \cdot g= & \\ & {[-3,6] } \\ & (-\infty, 6) \cup(6, \infty) \\ & {[-3,6) } \\ & (-\infty,-3) \cup(-3,6) \cup(6, \infty) \\ & (-\infty, \infty) \end{aligned} \]
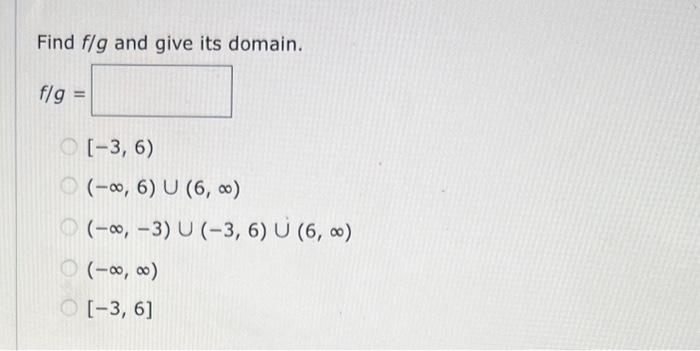
Find \( f / g \) and give its domain. \[ \begin{aligned} f / g= & \\ & {[-3,6) } \\ & (-\infty, 6) \cup(6, \infty) \\ & (-\infty,-3) \cup(-3,6) \cup(6, \infty) \\ & (-\infty, \infty) \\ & {[-3,6] } \end{aligned} \]
Expert Answer
(i) Consider the given functions, f(x)=x+3andg(x)=6?x Now, (f+g)(x)=f(x)+g(x) ?(f+g)(x)=x+3+6?x ?(f+g)(x)=x+3+6?x Now domain is, Non-negative values f