(Solved): Find the limit (enter 'DNE' if the limit does not exist) \[ \lim _{(x, y) \rightarrow(0,0)} \frac{( ...

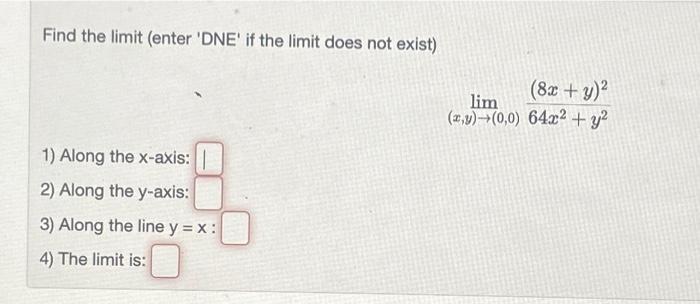
Find the limit (enter 'DNE' if the limit does not exist) \[ \lim _{(x, y) \rightarrow(0,0)} \frac{(8 x+y)^{2}}{64 x^{2}+y^{2}} \] 1) Along the \( x \)-axis: 2) Along the \( y \)-axis: 3) Along the line \( y=x \) : 4) The limit is: Examine the behavior of \( f(x, y)=\frac{9 x^{2} y}{8 x^{4}+y^{2}} \) as \( (x, y) \) approaches \( (0,0) \) Use "infinity" for " \( \infty \) " and "-infinity" for "- \( \infty \) ". Use "DNE" for "Does not exist". (a) Taking a linear approach to the origin along the \( y \)-axis, we find \[ \lim _{(x, y) \rightarrow(0,0), x=0}\left(\frac{9 x^{2} y}{8 x^{4}+y^{2}}\right)= \] (b) Taking a linear approach to the origin along the \( x \)-axis, we find \[ \lim _{(x, y) \rightarrow(0,0), y=0}\left(\frac{9 x^{2} y}{8 x^{4}+y^{2}}\right)= \] (c) Taking a linear approach to the origin along a line \( y=m x \) with \( m \neq 0 \) we find \[ \lim _{(x, y) \rightarrow(0,0), y=m x}\left(\frac{9 x^{2} y}{8 x^{4}+y^{2}}\right)=\lim _{x \rightarrow 0}()= \] Thought question: Do your answers to parts (a)-(c) allow you to conclude that the limit exists? (d) Taking an approach to the origin along the parabola \( y=x^{2} \) we find \[ \lim _{(x, y) \rightarrow(0,0), y=x^{2}}\left(\frac{9 x^{2} y}{8 x^{4}+y^{2}}\right)=\lim _{x \rightarrow 0}()= \] (e) Find the value of the limit. Be sure you can explain your answer. \[ \lim _{(x, y) \rightarrow(0,0)}\left(\frac{9 x^{2} y}{8 x^{4}+y^{2}}\right)= \]